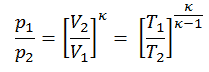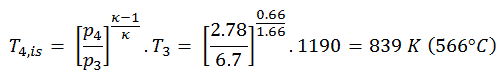Exemple: expansion isentropique dans une turbine à gaz
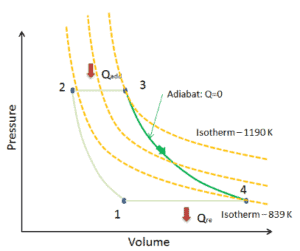
Supposons une expansion isentropique de l’hélium ( 3 → 4 ) dans une turbine à gaz . Comme l’hélium se comporte presque comme un gaz parfait , utilisez la loi des gaz parfaits pour calculer la température de sortie du gaz ( T 4, is ). Dans cette turbine, l’étage haute pression reçoit du gaz (point 3 sur la figure; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) d’un échangeur de chaleur et l’évacue vers un autre échangeur de chaleur, où la pression de sortie est p 4 = 2,78 MPa (point 4) .
Solution:
La température de sortie du gaz, T 4, est , peut être calculée en utilisant p, V, T Relation pour le processus isentropique (processus adiabatique réversible):
Dans cette équation, le facteur pour l’hélium est égal à κ = c p / c v = 1,66 . D’après l’équation précédente, la température de sortie du gaz, T 4 , est:

Voir aussi: Première loi de la thermodynamique
Voir aussi: Loi sur les gaz parfaits
Voir aussi: Qu’est-ce que l’enthalpie?
Exemple: expansion isentropique dans une turbine à gaz

Supposons le cycle de Brayton idéal qui décrit le fonctionnement d’un moteur thermique à pression constante . Les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérodynamique suivent également le cycle de Brayton.
Le cycle de Brayton idéal se compose de quatre processus thermodynamiques. Deux processus isentropiques et deux processus isobares.
- compression isentropique – l’air ambiant est aspiré dans le compresseur, où il est mis sous pression (1 → 2). Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- addition de chaleur isobare – l’air comprimé traverse ensuite une chambre de combustion, où le combustible est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- expansion isentropique – l’air chauffé sous pression se détend ensuite sur la turbine, cède son énergie. Le travail effectué par turbine est donné par W T = H 4 – H 3
- rejet de chaleur isobare – la chaleur résiduelle doit être rejetée afin de fermer le cycle. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Comme on peut le voir, nous pouvons décrire et calculer (par exemple l’ efficacité thermique ) de tels cycles (de même pour le cycle de Rankine ) en utilisant des enthalpies .
Voir aussi: Efficacité thermique du cycle de Brayton
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci