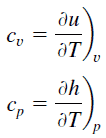Quelle est le première principe de la thermodynamique – Définition

Dans les mots:

Formulaire d’équation:

∆E _int = Q – W

où E _int représente l’ énergie interne du matériau, qui ne dépend que de l’ état du matériau (température, pression et volume). Q est la chaleur nette ajoutée au système et W est le travail net effectué par le système. Nous devons être prudents et cohérents en suivant les conventions de signe pour Q et W. Parce que W dans l’équation est le travail effectué par le système, alors si le travail est effectué sur le système, W sera négatif et E _int augmentera.

De même, Q est positif pour la chaleur ajoutée au système, donc si la chaleur quitte le système, Q est négative. Cela nous dit ce qui suit: L’ énergie interne d’un système a tendance à augmenter si la chaleur est absorbée par le système ou si un travail positif est effectué sur le système. Inversement, l’énergie interne a tendance à diminuer si la chaleur est perdue par le système ou si un travail négatif est effectué sur le système. Il faut ajouter que Q et W dépendent du chemin, tandis que E _int est indépendant du chemin.

Forme différentielle:

dE _int = dQ – dW

L’énergie interne E _int d’un système a tendance à augmenter si de l’énergie est ajoutée sous forme de chaleur Q et a tendance à diminuer si de l’énergie est perdue en tant que travail W effectué par le système.

Première loi en termes d’enthalpie dH = dQ + Vdp

L’ enthalpie est définie comme étant la somme de l’ énergie interne E plus le produit de la pression p et de volume V . Dans de nombreuses analyses thermodynamiques, la somme de l’énergie interne U et du produit de la pression p et du volume V apparaît, il est donc commode de donner à la combinaison un nom, une enthalpie et un symbole distinct, H.

H = U + pV

Voir aussi: Enthalpie

La première loi de la thermodynamique en termes d’ enthalpie nous montre pourquoi les ingénieurs utilisent l’enthalpie dans les cycles thermodynamiques (par exemple le cycle de Brayton ou le cycle de Rankine ).

La forme classique de la loi est l’équation suivante:

dU = dQ – dW

Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites .

Puisque H = U + pV , donc dH = dU + pdV + Vdp et nous substituons dU = dH – pdV – Vdp dans la forme classique de la loi:dH – pdV – Vdp = dQ – pdV

Nous obtenons la loi en matière d’enthalpie:

dH = dQ + Vdp

ou

dH = TdS + Vdp

Dans cette équation, le terme Vdp est un travail de processus d’écoulement. Ce travail,   Vdp , est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp» , c’est-à-dire un changement de pression. Il n’y a aucun changement dans le volume de contrôle . Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:

Processus isobare (Vdp = 0):

dH = dQ      →      Q = H ₂ – H ₁

À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:

Processus isentropique (dQ = 0):

dH = Vdp      →      W = H ₂ – H ₁

Il est évident, il sera très utile dans l’analyse des deux cycles thermodynamiques utilisés en génie énergétique, c’est-à-dire dans le cycle de Brayton et le cycle de Rankine.

Exemple: Première loi de la thermodynamique et cycle de Brayton

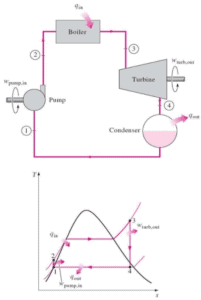
Supposons le cycle de Brayton idéal qui décrit le fonctionnement d’un moteur thermique à pression constante . Les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérodynamique suivent également le cycle de Brayton. Ce cycle comprend quatre processus thermodynamiques:

1. 

   compression isentropique – l’air ambiant est aspiré dans le compresseur, où il est mis sous pression (1 → 2). Le travail requis pour le compresseur est donné par W _C = H ₂ – H ₁ .

2. addition de chaleur isobare – l’air comprimé traverse ensuite une chambre de combustion, où le combustible est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q _add = H ₃ – H ₂
3. expansion isentropique – l’air chauffé sous pression se détend ensuite sur la turbine, cède son énergie. Le travail effectué par turbine est donné par W _T = H ₄ – H ₃
4. rejet de chaleur isobare – la chaleur résiduelle doit être rejetée afin de fermer le cycle. La chaleur nette rejetée est donnée par Q _re = H ₄ – H ₁

Comme on peut le voir, nous pouvons décrire et calculer (par exemple l’efficacité thermodynamique) de tels cycles (de même pour le cycle de Rankine ) en utilisant des enthalpies .

Énergie interne

En thermodynamique, l’énergie interne (également appelée énergie thermique ) est définie comme l’énergie associée aux formes microscopiques d’énergie . C’est une quantité importante , cela dépend de la taille du système ou de la quantité de substance qu’il contient. L’unité SI d’ énergie interne est le joule (J) . Il s’agit de l’énergie contenue dans le système, à l’exclusion de l’énergie cinétique de mouvement du système dans son ensemble et de l’énergie potentielle du système. Les formes microscopiques d’énergie comprennent celles dues à la rotation , aux vibrations, à la translation et aux interactionsparmi les molécules d’une substance. Aucune de ces formes d’énergie ne peut être mesurée ou évaluée directement, mais des techniques ont été développées pour évaluer la variation de la somme totale de toutes ces formes microscopiques d’énergie.

De plus, l’énergie peut être stockée dans les liaisons chimiques entre les atomes qui composent les molécules. Ce stockage d’énergie au niveau atomique comprend l’énergie associée aux états orbitaux des électrons, au spin nucléaire et aux forces de liaison dans le noyau.

Énergie microscopique

L’énergie interne implique de l’énergie à l’ échelle microscopique . Elle peut être divisée en énergie potentielle microscopique, U _pot , et énergie cinétique microscopique, U _kin , composants:

U = U _pot + U _kin

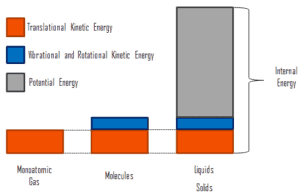où l’énergie cinétique microscopique, U _kin , implique les mouvements de toutes les particules du système par rapport au cadre du centre de masse. Pour un gaz monatomique idéal , ce n’est que l’ énergie cinétique de translation du mouvement linéaire des atomes. Les particules monoatomiques ne tournent pas et ne vibrent pas. Le comportement du système est bien décrit par la théorie cinétique des gaz. La théorie cinétique est basée sur le fait que lors d’une collision élastique entre une molécule à haute énergie cinétique et une à faible énergie cinétique, une partie de l’énergie sera transférée à la molécule d’énergie cinétique inférieure. Cependant, pour les gaz polyatomiques il y a rotation etl’énergie cinétique vibrationnelle aussi.

L’énergie potentielle microscopique, U _pot , implique les liaisons chimiques entre les atomes qui composent les molécules, les forces de liaison dans le noyau ainsi que les champs de force physiques au sein du système (par exemple les champs électriques ou magnétiques).

Dans les liquides et les solides, il existe une composante importante d’énergie potentielle associée aux forces d’attraction intermoléculaires .

Chaleur et travail

Nous avons vu que l’énergie interne change avec Q , qui est la chaleur nette ajoutée au système et W , qui est le travail net effectué par le système. Nous examinons maintenant comment le travail effectué par et la chaleur ajoutée au système pendant un processus thermodynamique dépendent des détails de la façon dont le processus se déroule.

La chaleur en thermodynamique

Alors que l’énergie interne fait référence à l’énergie totale de toutes les molécules à l’intérieur de l’objet, la chaleur est la quantité d’énergie circulant d’un corps à un autre spontanément en raison de leur différence de température. La chaleur est une forme d’énergie, mais c’est de l’ énergie en transit . La chaleur n’est pas la propriété d’un système. Cependant, le transfert d’énergie sous forme de chaleur se produit au niveau moléculaire en raison d’une différence de température .

Considérons un bloc de métal à haute température, composé d’atomes qui oscillent intensément autour de leur position moyenne. Aux basses températures , les atomes continuent d’osciller, mais avec moins d’intensité . Si un bloc de métal plus chaud est mis en contact avec un bloc plus froid, les atomes oscillant intensément au bord du bloc plus chaud dégagent son énergie cinétique aux atomes moins oscillants au bord du bloc froid. Dans ce cas, il y a un transfert d’énergie entre ces deux blocs et des flux de chaleur du bloc le plus chaud vers le bloc le plus froid par ces vibrations aléatoires.

En général, lorsque deux objets sont mis en contact thermique , la chaleur circule entre eux jusqu’à ce qu’ils s’équilibrent . Lorsqu’il existe une différence de température , la chaleur circule spontanément du système le plus chaud vers le système le plus froid . Le transfert de chaleur se produit par conduction ou par rayonnement thermique . Lorsque le flux de chaleur s’arrête , on dit qu’ils sont à la même température . On dit alors qu’ils sont en équilibre thermique .

Comme pour le travail, la quantité de chaleur transférée dépend du chemin et non pas simplement des conditions initiales et finales du système. Il existe en fait plusieurs façons de transporter le gaz de l’état i à l’état f.

De même, comme pour le travail, il est important de faire la distinction entre la chaleur ajoutée à un système de son environnement et la chaleur retirée d’un système à son environnement. Q est positif pour la chaleur ajoutée au système, donc si la chaleur quitte le système, Q est négatif. Parce que W dans l’équation est le travail effectué par le système, alors si le travail est effectué sur le système, W sera négatif et E _int augmentera.

Le symbole q est parfois utilisé pour indiquer la chaleur ajoutée ou retirée d’un système par unité de masse . Il est égal à la chaleur totale (Q) ajoutée ou retirée divisée par la masse (m).

Capacité thermique

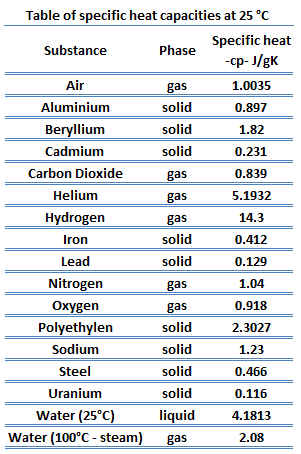Différentes substances sont affectées à différentes grandeurs par l’ ajout de chaleur . Lorsqu’une quantité donnée de chaleur est ajoutée à différentes substances, leurs températures augmentent de différentes quantités. Cette constante de proportionnalité entre la chaleur Q que l’objet absorbe ou perd et la variation de température T résultante de l’objet est appelée capacité calorifique C d’un objet.

C = Q / ΔT

La capacité calorifique est une propriété étendue de la matière, ce qui signifie qu’elle est proportionnelle à la taille du système. La capacité calorifique C a l’unité d’énergie par degré ou d’énergie par kelvin. Lorsqu’elle exprime le même phénomène qu’une propriété intensive , la capacité thermique est divisée par la quantité de substance, de masse ou de volume, donc la quantité est indépendante de la taille ou de l’étendue de l’échantillon.

La capacité thermique spécifique

La capacité thermique d’une substance par unité de masse est appelée capacité thermique spécifique (c _p ) de la substance. L’indice p indique que la capacité thermique et la capacité thermique spécifique s’appliquent lorsque la chaleur est ajoutée ou retirée à pression constante .

c _p = Q / mΔT

Capacité thermique spécifique du gaz parfait

Dans le modèle de gaz parfait , les propriétés intensives c _v et c _p sont définies pour les substances compressibles pures et simples comme des dérivées partielles de l’ énergie interne u (T, v) et de l’ enthalpie h (T, p) , respectivement:

où les indices v et p désignent les variables maintenues fixes pendant la différenciation. Les propriétés c _v et c _p sont appelées chaleurs spécifiques (ou capacités calorifiques ) car dans certaines conditions particulières, elles relient le changement de température d’un système à la quantité d’énergie ajoutée par transfert de chaleur. Les unités SI sont J / kg K ou J / mole K . Deux chaleurs spécifiques sont définies pour les gaz, une pour un volume constant (c _v ) et une pour une pression constante (c _p ) .

Selon la première loi de la thermodynamique , pour un procédé à volume constant avec un gaz parfait monatomique, la chaleur spécifique molaire sera:

C _v = 3 / 2R = 12,5 J / mol K

car

U = 3 / 2nRT

On peut déduire que la chaleur spécifique molaire à pression constante est:

C _p = C _v + R = 5 / 2R = 20,8 J / mol K

Ce C _p est supérieur à la chaleur spécifique molaire à volume constant C _v , car il faut désormais fournir de l’énergie non seulement pour élever la température du gaz mais aussi pour que le gaz fonctionne car dans ce cas le volume change.

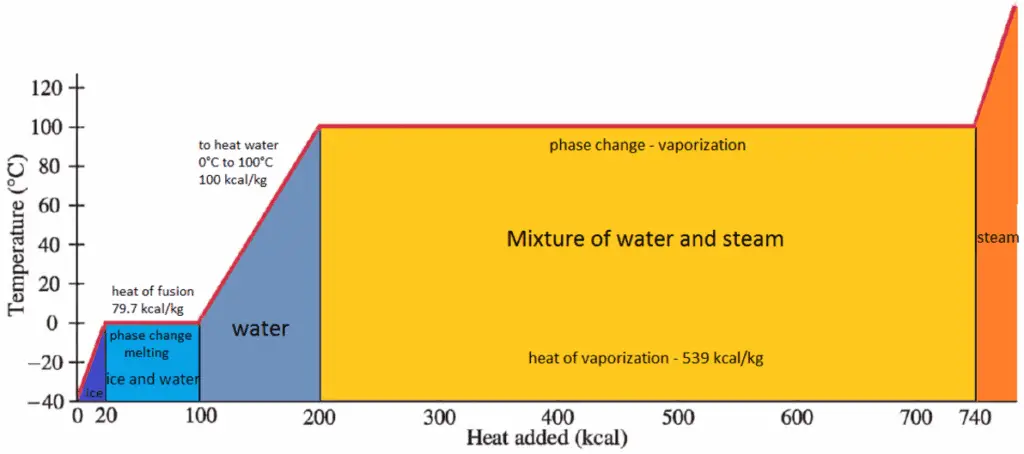
La chaleur latente de vaporisation

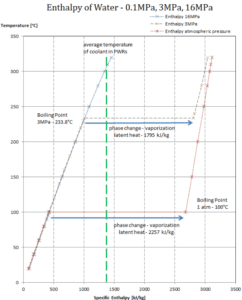
En général, lorsqu’un matériau change de phase du solide au liquide, ou du liquide au gaz, une certaine quantité d’énergie est impliquée dans ce changement de phase. En cas de changement de phase liquide en gaz, cette quantité d’énergie est connue sous le nom d’ enthalpie de vaporisation , (symbole ∆H _vap ; unité: J) également connue sous le nom de chaleur (latente) de vaporisation ou chaleur d’évaporation. La chaleur latente est la quantité de chaleur ajoutée ou retirée d’une substance pour produire un changement de phase. Cette énergie décompose les forces d’attraction intermoléculaires, et doit également fournir l’énergie nécessaire à l’expansion du gaz (le travail pΔV). Lorsque de la chaleur latente est ajoutée, aucun changement de température ne se produit. L’enthalpie de vaporisation est fonction de la pression à laquelle cette transformation a lieu.

Chaleur latente de vaporisation – eau à 0,1 MPa (pression atmosphérique)

h _lg = 2257 kJ / kg

Chaleur latente de vaporisation – eau à 3 MPa (pression à l’intérieur d’un générateur de vapeur)

h _lg = 1795 kJ / kg

Chaleur latente de vaporisation – eau à 16 MPa (pression à l’intérieur d’un pressuriseur )

h _lg = 931 kJ / kg

La chaleur de vaporisation diminue avec l’augmentation de la pression, tandis que le point d’ébullition augmente. Elle disparaît complètement à un certain point appelé le point critique . Au-dessus du point critique, les phases liquide et vapeur sont indiscernables et la substance est appelée fluide supercritique .

La chaleur de vaporisation est la chaleur nécessaire pour vaporiser complètement une unité de liquide saturé (ou condenser une unité de masse de vapeur saturée) et elle est égale à h _lg = h _g – h _l .

La chaleur nécessaire pour faire fondre (ou geler) une masse unitaire à la substance à pression constante est la chaleur de fusion et est égale à h _sl = h _l – h _s , où h _s est l’enthalpie du solide saturé et h _l est l’enthalpie du liquide saturé.

Travail en thermodynamique

En thermodynamique, le travail effectué par un système est l’énergie transférée par le système à son environnement. L’énergie cinétique, l’énergie potentielle et l’énergie interne sont des formes d’énergie qui sont les propriétés d’un système. Le travail est une forme d’énergie , mais c’est de l’ énergie en transit . Un système ne contient aucun travail, le travail est un processus effectué par ou sur un système. En général, le travail est défini pour les systèmes mécaniques comme l’action d’une force sur un objet à travers une distance.

W = F. ré

où:

W = travail (J)

F = force (N)

d = déplacement (m)

pΔV travail

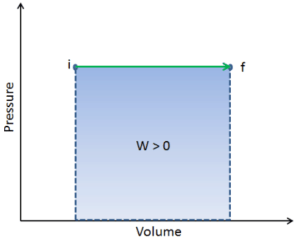
Le travail pression-volume (ou travail pΔV ) se produit lorsque le volume V d’un système change. Le travail pΔV est égal à l’aire sous la courbe de processus tracée sur le diagramme pression-volume. Il est également connu comme l’ ouvrage de délimitation . Le travail aux limites  se produit parce que la masse de la substance contenue dans les limites du système provoque une force, la pression multipliée par la surface, pour agir sur la surface des limites et la faire bouger. Le travail aux limites  (ou  travail pΔV ) se produit lorsque le  volume V d’un système change . Il est utilisé pour calculer le travail de déplacement du piston dans un  système fermé    . C’est ce qui se produit lorsque de la  vapeur ou du gaz contenu dans un piston-cylindre se dilate contre le piston et force le piston à se déplacer.

Exemple:

Considérons un piston sans friction qui est utilisé pour fournir une pression constante de 500 kPa en une vapeur contenant de cylindre ( vapeur surchauffée ) d’un volume de 2 m ³  à 500 K .

Calculez la température finale, si 3000 kJ de chaleur sont ajoutés.

Solution:

En utilisant des tables à vapeur, nous savons que l’ enthalpie spécifique de cette vapeur (500 kPa; 500 K) est d’environ 2912 kJ / kg . Étant donné qu’à cette condition, la vapeur a une densité de 2,2 kg / m ³ , alors nous savons qu’il y a environ 4,4 kg de vapeur dans le piston à l’enthalpie de 2912 kJ / kg x 4,4 kg = 12812 kJ .

Lorsque nous utilisons simplement Q = H ₂ – H ₁ , l’enthalpie de vapeur résultante sera alors:

H ₂ = H ₁ + Q = 15812 kJ

A partir des tables à vapeur , une telle vapeur surchauffée (15812 / 4,4 = 3593 kJ / kg) aura une température de 828 K (555 ° C) . Comme à cette enthalpie, la vapeur a une densité de 1,31 kg / m ³ , il est évident qu’elle a augmenté d’environ 2,2 / 1,31 = 1,67 (+ 67%). Par conséquent, le volume résultant est de 2 m ³ x 1,67 = 3,34 m ³ et ∆V = 3,34 m ³ – 2 m ³ = 1,34 m ³ .

La partie p∆V de l’enthalpie, c’est-à-dire le travail effectué est:

W = p∆V = 500 000 Pa x 1,34 m ³ = 670 kJ

———–

Pendant le changement de volume , la pression et la température peuvent également changer. Pour calculer de tels processus, nous aurions besoin de savoir comment la pression varie avec le volume pour le processus réel par lequel le système passe de l’état i à l’état f . La première loi de la thermodynamique et du travail peut alors s’exprimer comme:

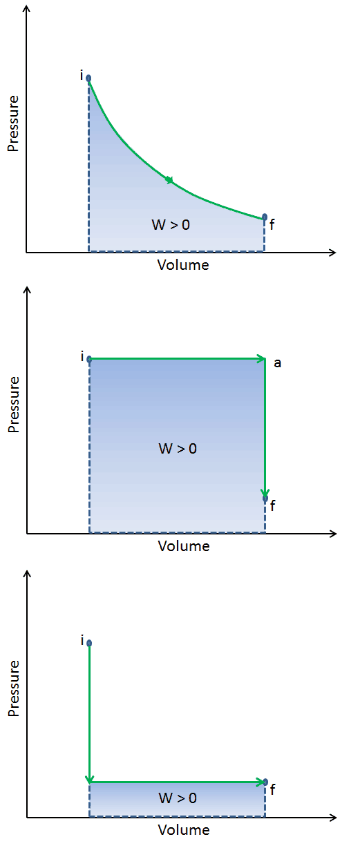
Lorsqu’un système thermodynamique passe d’un état initial à un état final , il passe par une série d’états intermédiaires . Nous appelons cette série d’états un chemin . Il existe toujours une infinité de possibilités différentes pour ces états intermédiaires. Quand ce sont tous des états d’équilibre, le chemin peut être tracé sur un diagramme pV . L’une des conclusions les plus importantes est que:

Le travail effectué par le système dépend non seulement des états initial et final, mais aussi des états intermédiaires, c’est-à-dire du chemin.

Q et W dépendent du chemin, tandis que ΔE _int est indépendant du chemin. Comme le montre l’image (diagramme pV), le travail est une variable dépendante du chemin. La zone bleue représente le travail pΔV effectué par un système lorsqu’il passe d’un état initial i à un état final f. Le travail W est positif car le volume du système augmente. Le deuxième processus montre que le travail est plus important et que cela dépend du chemin du processus.

De plus, nous pouvons faire passer le système à travers une série d’états formant une boucle fermée , tels que i ⇒ f ⇒ i . Dans ce cas, l’ état final est le même que l’état initial , mais le travail total effectué par le système n’est pas nul . Une valeur positive pour le travail indique que le travail est effectué par le système sur son environnement. Une valeur négative indique que le travail est effectué sur le système par son environnement.

Exemple: travaux spécifiques aux turbines

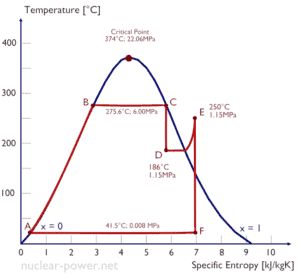
Un étage haute pression de turbine à vapeur fonctionne à l’état stable avec des conditions d’entrée de   6 MPa , t = 275,6 ° C , x = 1 (point C). La vapeur sort de cet étage de turbine à une pression de 1,15 MPa , 186 ° C et x = 0,87 (point D). Calculez la différence d’enthalpie entre ces deux états. Déterminez le transfert de travail spécifique.

L’ enthalpie pour l’état C peut être prélevée directement dans les tables de vapeur , tandis que l’enthalpie pour l’état D doit être calculée en utilisant la qualité de la vapeur :

h _{1, humide} = 2785 kJ / kg

h _{2, humide} = h _{2, s} x + (1 – x) h _{2, l}  = 2782. 0,87 + (1 – 0,87). 790 = 2420 + 103 = 2523 kJ / kg

Δh = 262 kJ / kg

Puisque dans le processus adiabatique dh = dw , Δh = 262 kJ / kg est le travail spécifique de la turbine .

Quatre cas particuliers de le première principe de la thermodynamique

La première loi de la thermodynamique trouve application dans plusieurs cas particuliers:

Processus adiabatique:

Un processus adiabatique est un processus dans lequel il n’y a pas de transfert de chaleur dans ou hors du système. Elle se produit très rapidement ou un système est bien isolé , aucun transfert d’énergie car la chaleur se produit entre le système et son environnement. Donc dQ = 0 dans le première principe de la thermodynamique, qui est alors:

dQ = 0, dE _int = – dW

Processus isochorique:

Un processus isochore est un processus dans lequel il n’y a pas de changement de volume . Un processus isochore est un processus à volume constant. Lorsque le volume d’un système thermodynamique est constant, il ne fonctionne pas sur son environnement. Donc dW = 0 dans le première principe de la thermodynamique, qui est alors:

dW = 0, dE _int = dQ

Dans un processus isochore , toute l’énergie ajoutée sous forme de chaleur (c’est-à-dire Q est positive) reste dans le système sous forme d’augmentation de l’énergie interne ( augmentation de la température ).

Processus cyclique:

Un processus qui ramène finalement un système à son état initial est appelé processus cyclique . À la fin d’un cycle, toutes les propriétés ont la même valeur qu’au début.

Pour un tel processus, l’état final est le même que l’état initial, et donc le changement d’énergie interne total doit être nul . La vapeur (eau) qui circule dans une boucle de refroidissement fermée subit un cycle. La première loi de la thermodynamique est alors:

dE _int = 0, dQ = dW

Ainsi, le travail net effectué au cours du processus doit être exactement égal à la quantité nette d’énergie transférée sous forme de chaleur.

Expansion gratuite:

Il s’agit d’un  processus adiabatique dans lequel aucun transfert de chaleur ne se produit entre le système et son environnement et aucun travail n’est effectué sur ou par le système. Ces types de processus adiabatiques sont appelés expansion libre . Il s’agit d’un processus irréversible dans lequel un gaz se détend dans une chambre sous vide isolée. Il est également appelé expansion Joule . Pour un gaz parfait, la température ne change pas (voir: Deuxième loi de Joule ), cependant, les vrais gaz subissent un changement de température pendant la détente libre. En expansion libre Q = W = 0, et le première principe exige que:

dE _int = 0

Une expansion libre ne peut pas être tracée sur un diagramme PV, car le processus est rapide et non quasi statique. Les états intermédiaires ne sont pas des états d’équilibre, et donc la pression n’est pas clairement définie.