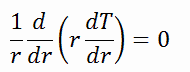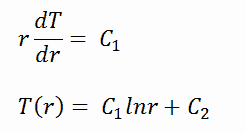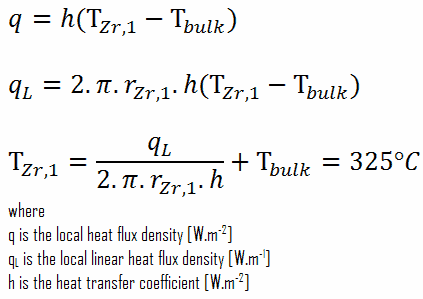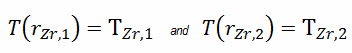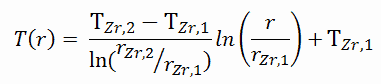O que é a distribuição de temperatura no revestimento de combustível – Definição

Distribuição de temperatura no revestimento de combustível

O revestimento é a camada externa das barras de combustível, situada entre o líquido de arrefecimento do reator e o combustível nuclear (isto é, granulados de combustível ). É feito de um material resistente à corrosão com seção transversal de baixa absorção para nêutrons térmicos, geralmente liga de zircônio . O revestimento evita que os produtos de fissão radioativa escapem da matriz de combustível para o líquido de arrefecimento do reator e os contaminem. O revestimento constitui uma das barreiras na abordagem de ‘ defesa em profundidade ‘.

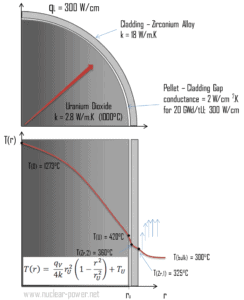
Considere o revestimento de combustível do raio interno r _{Zr, 2} = 0,408 cm e raio externo r _{Zr, 1} = 0,465 cm . Em comparação com o pellet de combustível, quase não há geração de calor no revestimento do combustível (o revestimento é levemente aquecido pela radiação ). Todo o calor gerado no combustível deve ser transferido por condução através do revestimento e, portanto, a superfície interna é mais quente que a superfície externa.

Para encontrar a distribuição de temperatura através do revestimento, precisamos resolver a equação de condução de calor . Devido à simetria na direção z e na direção azimutal, podemos separar as variáveis ​​e simplificar esse problema para um problema unidimensional. Assim, resolveremos apenas a temperatura em função do raio T (r). Neste exemplo, assumiremos que não existe estritamente geração de calor no revestimento. Para condutividade térmica constante, k, a forma apropriada da equação de calor cilíndrica é:

A solução geral desta equação é:

onde C ₁ e C ₂ são as constantes de integração.

1)

Calcule a distribuição de temperatura, T (r), neste revestimento de combustível, se:

• a temperatura na superfície interna do revestimento é T _{Zr, 2} = 360 ° C
• a temperatura do líquido de arrefecimento do reator nesta coordenada axial é T a _granel = 300 ° C
• o coeficiente de transferência de calor (convecção; fluxo turbulento) é h = 41 kW / m ² .K.
• a condutividade média do material é k = 18 W / mK
• a taxa linear de calor do combustível é q _L = 300 W / cm e, portanto, a taxa volumétrica de calor é q _V = 597 x 10 ⁶ W / m ³

A partir da relação básica para transferência de calor por convecção, podemos calcular a superfície externa do revestimento como:

Como pode ser visto, também neste caso, fornecemos temperaturas de superfície T _{Zr, 1} e T _{Zr, 2} . Isso corresponde à condição de limite de Dirichlet. As constantes podem ser avaliadas usando a substituição na solução geral e têm a forma:

Resolvendo C ₁ e C ₂ e substituindo na solução geral, obtemos então:

∆T – superfície de revestimento – refrigerante

O conhecimento detalhado da geometria, raio externo do revestimento, taxa de calor linear, coeficiente de transferência de calor por convecção e temperatura do líquido de refrigeração determina ∆T entre o líquido de arrefecimento (T a _granel ) e a superfície do revestimento (T _{Zr, 1} ). Portanto, podemos calcular a temperatura da superfície do revestimento (T _{Zr, 1} ) simplesmente usando a Lei de Newton :

∆T no revestimento do combustível

O conhecimento detalhado da geometria, raio externo e interno do revestimento, taxa de calor linear e temperatura da superfície do revestimento (T _{Zr, 1} ) determina ∆T entre as superfícies externa e interna do revestimento. Portanto, podemos calcular a temperatura da superfície interna do revestimento (T _{Zr, 2} ) simplesmente usando a Lei de Fourier :