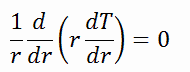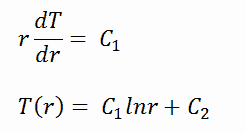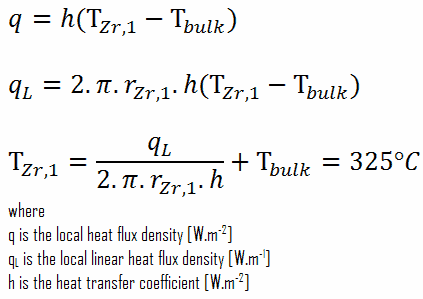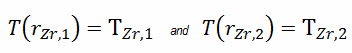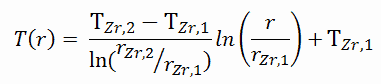Temperaturverteilung in der Kraftstoffhülle
Mantel ist die äußere Schicht der Brennstäbe, die zwischen dem Reaktorkühlmittel und dem Kernbrennstoff (dh Brennstoffpellets ) steht. Es besteht aus einem korrosionsbeständigen Material mit geringem Absorptionsquerschnitt für thermische Neutronen, üblicherweise aus einer Zirkoniumlegierung . Die Ummantelung verhindert, dass radioaktive Spaltprodukte aus der Brennstoffmatrix in das Reaktorkühlmittel gelangen und dieses verunreinigen. Verkleidungen sind eines der Hindernisse für einen vertieften Verteidigungsansatz .
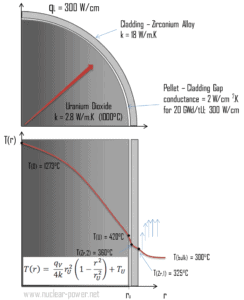
Betrachten Sie die Kraftstoffhülle mit dem Innenradius r Zr, 2 = 0,408 cm und dem Außenradius r Zr, 1 = 0,465 cm . Im Vergleich zu Brennstoffpellets entsteht in der Brennstoffhülle kaum Wärme (die Hülle wird durch Strahlung leicht erwärmt ). Die gesamte im Kraftstoff erzeugte Wärme muss durch Leitung durch die Ummantelung übertragen werden, und daher ist die Innenfläche heißer als die Außenfläche.
Um die Temperaturverteilung durch die Ummantelung zu finden, müssen wir die Wärmeleitungsgleichung lösen . Aufgrund der Symmetrie in z-Richtung und in azimutaler Richtung können wir Variablen trennen und dieses Problem zu einem eindimensionalen Problem vereinfachen. Wir lösen also nur die Temperatur als Funktion des Radius T (r). In diesem Beispiel wird davon ausgegangen, dass innerhalb der Verkleidung keine Wärme entsteht. Für eine konstante Wärmeleitfähigkeit ist k die geeignete Form der zylindrischen Wärmegleichung:
Die allgemeine Lösung dieser Gleichung lautet:
wobei C 1 und C 2 die Integrationskonstanten sind.
1)
Berechnen Sie die Temperaturverteilung T (r) in dieser Kraftstoffhülle, wenn:
- Die Temperatur an der Innenfläche der Ummantelung beträgt T Zr, 2 = 360 ° C.
- Die Temperatur des Reaktorkühlmittels an dieser axialen Koordinate beträgt T Volumen = 300 ° C.
- Der Wärmeübergangskoeffizient (Konvektion; turbulente Strömung) beträgt h = 41 kW / m 2 .K.
- Die Leitfähigkeit des gemittelten Materials beträgt k = 18 W / mK
- Die lineare Heizrate des Brennstoffs beträgt q L = 300 W / cm und somit beträgt die volumetrische Heizrate q V = 597 × 10 6 W / m 3
Aus der Grundbeziehung für die Wärmeübertragung durch Konvektion können wir die äußere Oberfläche der Ummantelung berechnen als:
Wie zu sehen ist, haben wir auch in diesem Fall Oberflächentemperaturen T Zr, 1 und T Zr, 2 angegeben . Dies entspricht der Dirichlet-Randbedingung. Die Konstanten können durch Substitution in die allgemeine Lösung bewertet werden und haben die Form:
Wenn wir nach C 1 und C 2 auflösen und in die allgemeine Lösung einsetzen, erhalten wir:
∆T – Verkleidungsfläche – Kühlmittel
Detaillierte Kenntnisse der Geometrie, des Außenmantelradius, der linearen Heizrate, des konvektiven Wärmeübergangskoeffizienten und der Kühlmitteltemperatur bestimmen ∆T zwischen dem Kühlmittel (T Bulk ) und der Manteloberfläche (T Zr, 1 ). Daher können wir die Manteloberflächentemperatur (T Zr, 1 ) einfach nach dem Newtonschen Gesetz berechnen :
∆T in der Kraftstoffverkleidung
Detaillierte Kenntnisse der Geometrie, des äußeren und inneren Radius der Verkleidung, der linearen Heizrate und der Temperatur der Verkleidungsoberfläche (T Zr, 1 ) bestimmen ∆T zwischen der äußeren und der inneren Oberfläche der Verkleidung. Daher können wir die Oberflächentemperatur des inneren Mantels (T Zr, 2 ) einfach nach dem Fourier-Gesetz berechnen :
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.