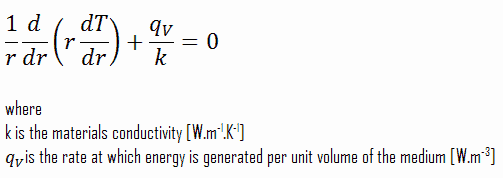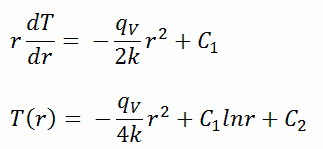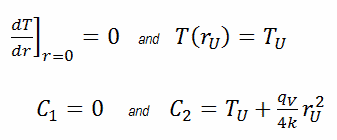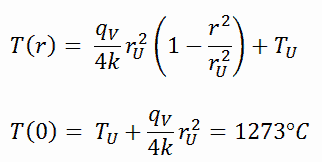O que é o perfil de temperatura – combustível nuclear – definição

Perfil de temperatura – combustível nuclear

Veja também: Geração de calor em reatores nucleares

Veja também: Temperatura da superfície do revestimento

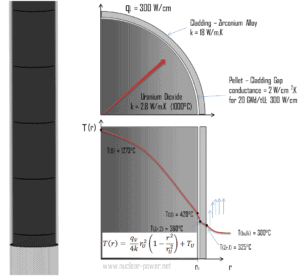
A maioria dos PWRs usa o combustível de urânio , que está na forma de dióxido de urânio . O dióxido de urânio é um sólido semicondutor preto com condutividade térmica muito baixa. Por outro lado, o dióxido de urânio tem um ponto de fusão muito alto e um comportamento bem conhecido. A UO ₂ é prensada em pastilhas cilíndricas , essas pastilhas são então sinterizadas no sólido.

Esses pellets cilíndricos são então carregados e encapsulados dentro de uma barra de combustível (ou pino de combustível), que é feita de ligas de zircônio devido à sua seção transversal de absorção muito baixa (ao contrário do aço inoxidável). A superfície do tubo, que cobre os pellets, é chamada de revestimento de combustível .

Veja também:  Condução térmica de dióxido de urânio

O comportamento térmico e mecânico dos pellets  e barras de combustível constitui uma das três principais disciplinas do projeto. O combustível nuclear é operado sob condições muito inóspitas (térmica, radiação, mecânica) e deve suportar mais do que as condições normais de operação. Por exemplo, as temperaturas no centro dos pellets de combustível atingem mais de 1000 ° C (1832 ° F) acompanhadas por liberações de gás de fissão. Portanto, o conhecimento detalhado da distribuição de temperatura em uma única barra de combustível é essencial para a operação segura do combustível nuclear. Nesta seção, estudaremos a equação de condução de calor em coordenadas cilíndricasusando a condição limite de Dirichlet com determinada temperatura da superfície (ou seja, usando a condição limite de Dirichlet). A análise abrangente do perfil de temperatura da barra de combustível será estudada em seção separada.

Temperatura na linha central de um pellet de combustível

Considere o pellet de combustível de raio r _U = 0,40 cm , no qual há geração uniforme e constante de calor por unidade de volume, q _V [W / m ³ ] . Em vez da taxa de calor volumétrica q _V [W / m ³ ], os engenheiros costumam usar a taxa de calor linear, q _L [W / m] , que representa a taxa de calor de um metro da barra de combustível. A taxa linear de calor pode ser calculada a partir da taxa volumétrica de calor por:

A linha central é tomada como a origem da coordenada r. Devido à simetria na direção z e na direção azimutal, podemos separar as variáveis ​​e simplificar esse problema para um problema unidimensional . Assim, resolveremos apenas a temperatura em função do raio T (r) . Para condutividade térmica constante , k, a forma apropriada da equação de calor cilíndrica é:

A solução geral desta equação é:

onde C ₁ e C ₂ são as constantes de integração.

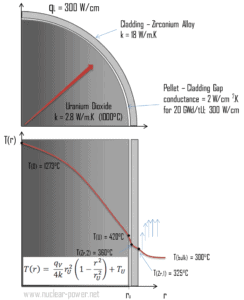Calcule a distribuição de temperatura, T (r) , neste sedimento de combustível, se:

• as temperaturas na superfície do sedimento de combustível são T _U = 420 ° C
• raio da pastilha de combustível r _U = 4 mm .
• a condutividade média do material é k = 2,8 W / mK (corresponde ao dióxido de urânio a 1000 ° C)
• a taxa de calor linear é q _L = 300 W / cm e, portanto, a taxa de calor volumétrica é q _V = 597 x 10 ⁶ W / m ³

Neste caso, a superfície é mantida a temperaturas dadas T _U . Isso corresponde à condição de limite de Dirichlet . Além disso, esse problema é termicamente simétrico e, portanto, também podemos usar a condição de contorno de simetria térmica . As constantes podem ser avaliadas usando a substituição na solução geral e têm a forma:

A distribuição de temperatura resultante e a temperatura da linha central (r = 0) (máxima) neste sedimento cilíndrico de combustível nessas condições de contorno específicas serão:

O fluxo de calor radial em qualquer raio, q _r [Wm ^-1 ], no cilindro pode, é claro, ser determinado usando a distribuição de temperatura e com a lei de Fourier . Observe que, com a geração de calor, o fluxo de calor não é mais independente de r.

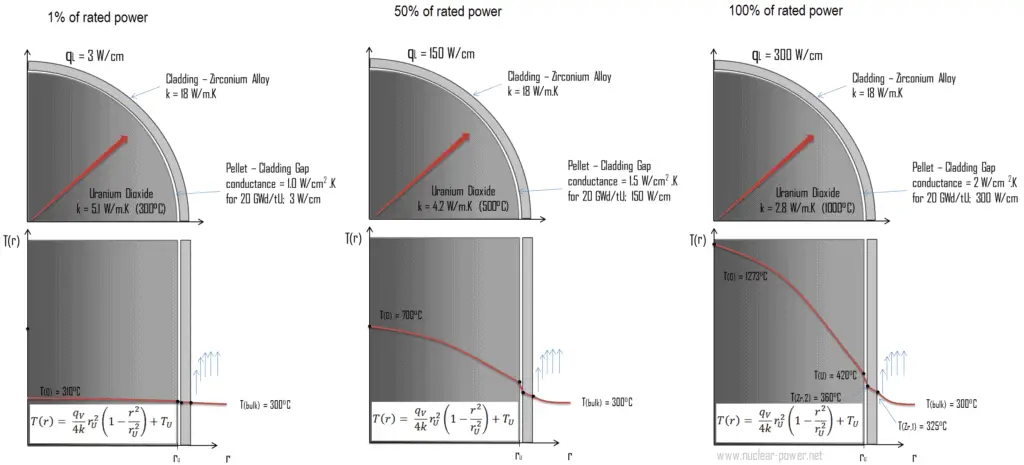
A figura a seguir mostra a distribuição de temperatura no pellet de combustível em vários níveis de potência.

______

A temperatura em um reator operacional varia de ponto a ponto dentro do sistema. Como consequência, há sempre uma vara de combustível e um volume local , que está mais quente  do que todo o resto. Para limitar esses locais quentes, os limites de potência máxima devem ser introduzidos. Os limites de potência máxima estão associados a uma crise de ebulição e às condições que podem causar o derretimento do pellet de combustível. No entanto, considerações metalúrgicas impõem limites superiores à temperatura do revestimento do combustível e do sedimento de combustível. Acima dessas temperaturasexiste o perigo de o combustível ser danificado. Um dos principais objetivos no projeto de reatores nucleares é fornecer a remoção do calor produzido no nível de potência desejado, garantindo que a temperatura máxima do combustível e a temperatura máxima do revestimento estejam sempre abaixo desses valores predeterminados.

Veja também:  Temperatura da superfície do revestimento