Teoria das Bombas – Equações de turbomáquinas de Euler
A equação da turbomáquina de Euler , ou às vezes chamada de equação da bomba de Euler , desempenha um papel central na turbomáquina , pois conecta o trabalho específico Y e a geometria e velocidades no impulsor. A equação é baseada nos conceitos de conservação do momento angular e conservação de energia .
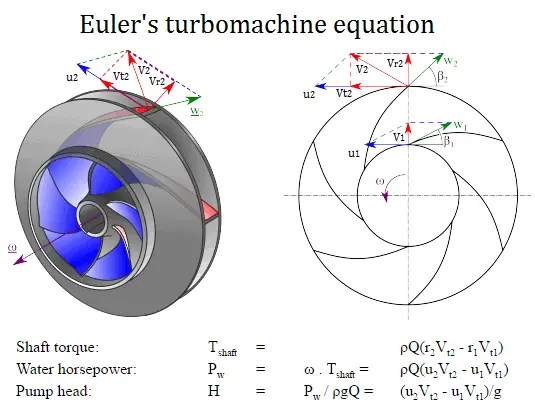
As equações da turbomáquina de Euler são:
Torque do eixo: T eixo = ρQ (r 2 V t2 – r 1 V t1 )
Cavalos-força da água: P w = ω. Eixo T = ρQ (u 2 V t2 – u 1 V t1 )
Cabeça da bomba: H = P w / ρgQ = (u 2 V t2 – u 1 V t1 ) / g
Onde
- r 1e r 2 são os diâmetros do impulsor na entrada e na saída, respectivamente.
- u 1 e u 2são as velocidades absolutas do impulsor (u 1 = r 1. ω) na entrada e na saída, respectivamente.
- V t1 e V t2 são as velocidades tangenciais do fluxo na entrada e na saída, respectivamente.
As equações da turbomáquina de Euler podem ser usadas para prever o impacto da alteração da geometria do impulsor na cabeça . Não importa quando lidamos com uma bomba ou uma turbina. Se o torque e a velocidade angular tiverem o mesmo sinal , o trabalho está sendo realizado no fluido (uma bomba ou compressor). Se o torque e a velocidade angular são de sinal oposto, o trabalho está sendo extraído do fluido (uma turbina). Assim, para o aspecto de projeto de turbinas e bombas , as equações de Euler são extremamente úteis.
Exemplo: Cálculo de desempenho da bomba
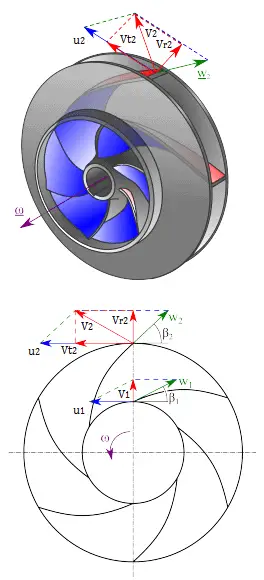Neste exemplo, veremos como prever
- a descarga do projeto
- cavalos-vapor de água
- a cabeça da bomba
de uma bomba centrífuga. Esses dados de desempenho serão derivados da equação de turbomáquina de Euler:
Torque do eixo: T eixo = ρQ (r 2 V t2 – r 1 V t1 )
Cavalos-força da água: P w = ω. Eixo T = ρQ (u 2 V t2 – u 1 V t1 )
Cabeça da bomba: H = P w / ρgQ = (u 2 V t2 – u 1 V t1 ) / g
São fornecidos os seguintes dados para uma bomba de água centrífuga:
- diâmetros do impulsor na entrada e na saída
- r 1 = 10 cm
- r 2 = 20 cm
- Velocidade = 1500 rpm (rotações por minuto)
- o ângulo da lâmina na entrada β 1 = 30 °
- o ângulo da lâmina na saída β 2 = 20 °
- suponha que as larguras da lâmina na entrada e na saída sejam: b 1 = b 2 = 4 cm .
Solução:
Primeiro, temos que calcular a velocidade radial do fluxo na saída. No diagrama de velocidade, a velocidade radial é igual a (assumimos que o fluxo entra exatamente normal ao impulsor, portanto o componente tangencial da velocidade é zero):
V r1 = u 1 tan 30 ° = ω r 1 tan 30 ° = 2π x (1500/60) x 0,1 x tan 30 ° = 9,1 m / s
O componente radial da velocidade de fluxo determina quanto a taxa de fluxo de volume está entrando no impulsor . Portanto, quando conhecemos V r1 na entrada, podemos determinar a descarga desta bomba de acordo com a seguinte equação. Aqui b 1 significa a largura da pá do impulsor na entrada.
Q = 2π.r 1 .b 1 .V r1 = 2π x 0,1 x 0,04 x 9,1 = 0,229 m 3 / s
Para calcular a potência de água (P w ) necessária, temos que determinar a velocidade do fluxo tangencial de saída V t2 , porque foi assumido que a velocidade tangencial de entrada V t1 é igual a zero.
A velocidade do fluxo radial de saída segue da conservação de Q :
Q = 2π.r 2 .b 2 .V r2 ⇒ V r2 = Q / 2π.r 2 .b 2 = 0,229 / (2π x 0,2 x 0,04) = 4,56 m / s
A partir do ângulo da lâmina de saída da figura ( triângulo da velocidade ), β 2 , pode ser facilmente representado da seguinte maneira.
berço β 2 = (u 2 – V t2 ) / V r2
e, portanto, a velocidade do fluxo tangencial de saída V t2 é:
V t2 = u 2 – V r2 . berço 20 ° = ω r 2 – V R2 . berço 20 ° = 2π x 1500/60 x 0,2 – 4,56 x 2,75 = 31,4 – 12,5 = 18,9 m / s.
A potência de água necessária é então:
P w = ρ Q u 2 V t2 = 1000 [kg / m 3 ] x 0,229 [m 3 / s] x 31,4 [m / s] x 18,9 [m / s] = 135900 W = 135,6 kW
e a cabeça da bomba é:
H ≈ P w / (ρ g Q) = 135900 / (1000 x 9,81 x 0,229) = 60,5 m
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
