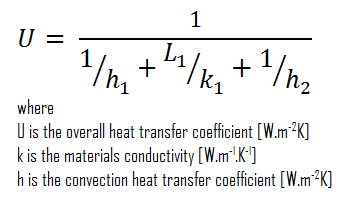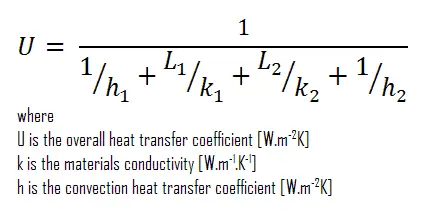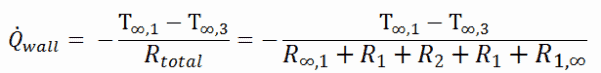O que é espuma de poliisocianurato – definição

Espuma de poliisocianurato

Espuma de poliisocianurato (PIR) , também conhecida como PIR , poliiso ou ISO, é muito semelhante à espuma de poliuretano. É também um polímero termoendurecível de células fechadas formado pela reação de um di- ou poli-isocianato com um poliol. A condutividade térmica pode ser menor que a da espuma de poliuretano. Espuma de poliisocianuratoé normalmente usado para painéis de face metálica, placas de teto, placas de parede de cavidades e isolamento de tubos. Os painéis de espuma PIR laminados com papel de alumínio puro em relevo são usados ​​para a fabricação de dutos pré-isolados que são usados ​​para sistemas de aquecimento, ventilação e ar condicionado. Por outro lado, o PIR não pode ser usado para isolar as paredes das cavidades existentes, pois não há espuma de PIR que possa ser injetada nas paredes existentes. Oferece ainda melhor estabilidade térmica e resistência à inflamabilidade do que a espuma de poliuretano.

Condutividade térmica da espuma de poliisocianurato

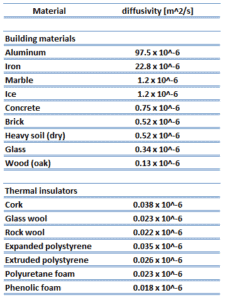Condutividade térmica é definida como a quantidade de calor (em watts) transferida através de uma área quadrada de material de determinada espessura (em metros) devido a uma diferença de temperatura . Quanto menor a condutividade térmica do material, maior a capacidade do material de resistir à transferência de calor e, portanto, maior a eficácia do isolamento. Os valores típicos de condutividade térmica para as espumas de poliisocianurato são entre 0,022 e 0.035W / m ∙ K .

Em geral, o isolamento térmico é baseado principalmente na condutividade térmica muito baixa dos gases . Os gases possuem más propriedades de condução térmica em comparação com líquidos e sólidos e, portanto, são um bom material para isolamento se puderem ser presos (por exemplo, em uma estrutura semelhante a espuma). Ar e outros gases geralmente são bons isolantes. Mas o principal benefício é na ausência de convecção. Portanto, muitos materiais isolantes (por exemplo, espuma de poliisocianurato ) funcionam simplesmente com um grande número de bolsas cheias de gás que impedem a convecção em grande escala .

A alternância entre bolsa de gás e material sólido faz com que o calor seja transferido através de muitas interfaces, causando uma rápida diminuição no coeficiente de transferência de calor.

Exemplo – Isolamento de Espuma de Poliisocianurato

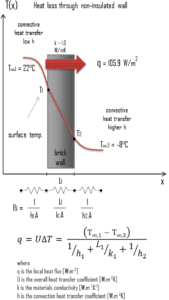Uma das principais fontes de perda de calor de uma casa é através das paredes. Calcule a taxa de fluxo de calor através de uma parede com 3 mx 10 m de área (A = 30 m ² ). A parede tem 15 cm de espessura (L ₁ ) e é feita de tijolos com condutividade térmica de k ₁ = 1,0 W / mK (isolador térmico ruim). Suponha que as temperaturas interna e externa sejam 22 ° C e -8 ° C, e os coeficientes de transferência de calor por convecção nos lados interno e externo sejam h ₁ = 10 W / m ² K e h ₂ = 30 W / m ²K, respectivamente. Observe que esses coeficientes de convecção dependem muito das condições ambientais e interiores (vento, umidade etc.).

1. Calcule o fluxo de calor ( perda de calor ) através desta parede não isolada.
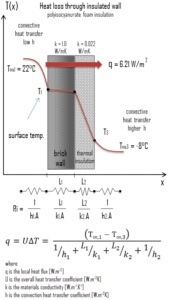
2. Agora assuma o isolamento térmico no lado externo desta parede. Use um  isolamento de espuma de poliisocianurato com 10 cm de espessura (L ₂ ) com a condutividade térmica de k ₂ = 0,022 W / mK e calcule o fluxo de calor ( perda de calor ) através dessa parede composta.

Solução:

Como foi escrito, muitos dos processos de transferência de calor envolvem sistemas compostos e até envolvem uma combinação de condução e convecção . Com estes sistemas compostos, muitas vezes é conveniente trabalhar com um coeficiente de transferência total de calor , conhecido como um factor-L . O fator U é definido por uma expressão análoga à lei do resfriamento de Newton :

O coeficiente geral de transferência de calor está relacionado à resistência térmica total e depende da geometria do problema.

1. parede nua

Assumindo a transferência de calor unidimensional através da parede plana e desconsiderando a radiação, o coeficiente geral de transferência de calor pode ser calculado como:

O coeficiente geral de transferência de calor é então:

U = 1 / (1/10 + 0,15 / 1 + 1/30) = 3,53 W / m ² K

O fluxo de calor pode ser calculado simplesmente como:

q = 3,53 [W / m ² K] x 30 [K] = 105,9 W / m ²

A perda total de calor através desta parede será:

q _perda = q. A = 105,9 [W / m ² ] x 30 [m ² ] = 3177W

2. parede compósita com isolamento térmico

Assumindo a transferência de calor unidimensional através da parede composta plana, sem resistência ao contato térmico e sem considerar a radiação, o coeficiente geral de transferência de calor pode ser calculado como:

O coeficiente geral de transferência de calor é então:

U = 1 / (1/10 + 0,15 / 1 + 0,1 / 0,022 + 1/30) = 0,207 W / m ² K

O fluxo de calor pode ser calculado simplesmente como:

q = 0,207 [W / m ² K] x 30 [K] = 6,21 W / m ²

A perda total de calor através desta parede será:

q _perda = q. A = 6,21 [W / m ² ] x 30 [m ² ] = 186 W

Como pode ser visto, uma adição de isolador térmico causa uma diminuição significativa nas perdas de calor. Deve ser adicionado, uma adição da próxima camada de isolador térmico não causa economias tão altas. Isso pode ser visto melhor no método de resistência térmica, que pode ser usado para calcular a transferência de calor através de paredes compostas . A taxa de transferência constante de calor entre duas superfícies é igual à diferença de temperatura dividida pela resistência térmica total entre essas duas superfícies.