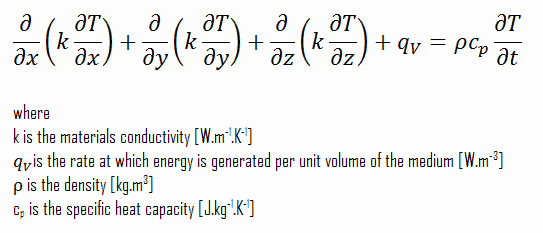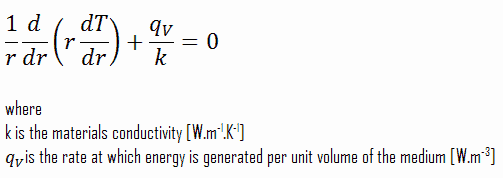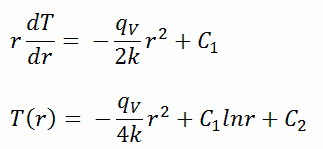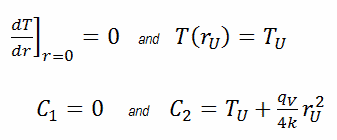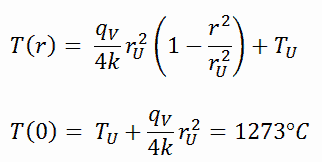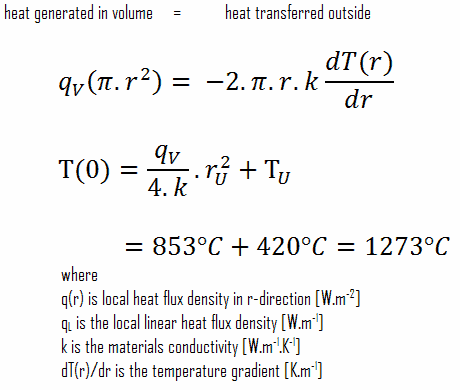O que é condução térmica – Condução térmica – Definição

Condução Térmica – Condução Térmica

A condução térmica , também chamada de condução térmica , ocorre dentro de um corpo ou entre dois corpos em contato sem o envolvimento do fluxo de massa e da mistura. É a troca microscópica direta da energia cinética das partículas através da fronteira entre dois sistemas. A transferência de calor por condução depende da “força” motriz da diferença de temperatura e da condutividade térmica (ou da resistência à transferência de calor). A condutividade térmica depende da natureza e das dimensões do meio de transferência de calor. Todos os problemas de transferência de calor envolvem a diferença de temperatura , a geometriae as propriedades físicas do objeto que está sendo estudado. Em problemas de transferência de calor por condução, o objeto em estudo geralmente é sólido.

Microscopicamente, esse modo de transferência de energia é atribuído ao fluxo livre de elétrons dos níveis de energia mais alto para o mais baixo, vibração da rede e colisão molecular . Considere um bloco de pedra  em alta temperatura, que consiste em átomos que oscilam intensamente em torno de suas posições médias. A baixas temperaturas , os átomos continuam a oscilar, mas com menos intensidade .Se um bloco de pedra mais quente é colocado em contato com um bloco mais frio, os átomos intensamente oscilantes na borda do bloco mais quente emitem sua energia cinética para os átomos menos oscilantes na borda do bloco frio. Nesse caso, há transferência de energia entre esses dois blocos e o calor flui do bloco mais quente para o mais frio por essas vibrações aleatórias. A visão moderna é atribuir a transferência de energia a ondas reticuladas induzidas pelo movimento atômico. Nos isoladores elétricos, a transferência de energia é exclusivamente através dessas ondas de treliça. Em um condutor, isso também se deve ao movimento de translação dos elétrons livres.

Veja também: Lei Zeroth da Termodinâmica

Em geral, os metais são geralmente bons condutores de energia térmica . Está intimamente associado à sua boa condutividade elétrica . Para metais, a condutividade térmica é bastante alta e os metais que são os melhores condutores elétricos também são os melhores condutores térmicos. Isto é devido à maneira como os metais se ligam quimicamente. As ligações metálicas possuem elétrons em movimento livre ( elétrons livres) que transferem energia térmica rapidamente através do metal. O fluido de elétrons de um sólido metálico condutor conduz a maior parte do fluxo de calor através do sólido. O fluxo de fônon ainda está presente, mas carrega menos energia. Esses mecanismos de condução térmica serão discutidos mais adiante.

Lei de Fourier de condução térmica

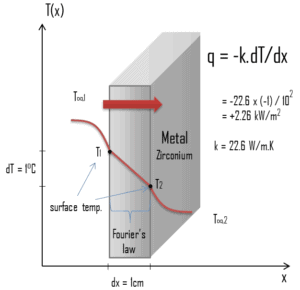
Os processos de transferência de calor podem ser quantificados em termos de equações de taxa apropriadas. A equação da taxa neste modo de transferência de calor é baseada na lei de condução térmica de Fourier . Esta lei estabelece que a taxa de tempo de transferência de calor através de um material é proporcional ao gradiente negativo na temperatura e à área, perpendicularmente àquele gradiente, através do qual o calor flui. Sua forma diferencial é:

Da mesma forma, como a lei de Fourier determina o fluxo de calor através de uma laje, ela também pode ser usada para determinar a diferença de temperatura, quando q é conhecido. Isso pode ser usado para o cálculo da temperatura no centro do pellet de combustível, como será mostrado nas seções a seguir.

Equação de Condução de Calor

Nas seções anteriores, tratamos especialmente da transferência de calor unidimensional em estado estacionário, que pode ser caracterizada pela lei de Fourier de condução de calor. Mas sua aplicabilidade é muito limitada. Esta lei pressupõe a transferência de calor em estado estacionário através de um corpo plano (observe que a lei de Fourier também pode ser derivada para coordenadas cilíndricas e esféricas), sem fontes de calor . É simplesmente a equação da taxa neste modo de transferência de calor, onde o gradiente de temperatura é conhecido.

Mas um grande problema na maioria das análises de condução é determinar o campo de temperatura em um meio resultante das condições impostas aos seus limites. Na engenharia, temos que resolver problemas de transferência de calor envolvendo diferentes geometrias e condições diferentes, como um elemento de combustível nuclear cilíndrico, que envolve fonte de calor interna ou a parede de uma contenção esférica. Esses problemas são mais complexos do que as análises planares que fizemos nas seções anteriores. Portanto, esses problemas serão o assunto desta seção, na qual a equação de condução de calor será introduzida e resolvida.

Veja também: Equação de calor

Equação de Condução de Calor – Forma Geral

A equação de condução de calor é uma equação diferencial parcial que descreve a distribuição de calor (ou o campo de temperatura ) em um determinado corpo ao longo do tempo. O conhecimento detalhado do campo de temperatura é muito importante na condução térmica através de materiais. Uma vez que essa distribuição de temperatura é conhecida, o fluxo de calor de condução em qualquer ponto do material ou em sua superfície pode ser calculado pela lei de Fourier .

A equação do calor é derivada da lei de Fourier e da conservação de energia . A lei de Fourier afirma que a taxa de tempo de transferência de calor através de um material é proporcional ao gradiente negativo na temperatura e à área, perpendicularmente àquele gradiente, através do qual o calor flui.

Uma mudança na energia interna por unidade de volume no material, ΔQ, é proporcional à mudança na temperatura, Δu. Isso é:

∆Q = ρ.c _p .∆T

Forma geral

Usando essas duas equações, podemos derivar a equação geral de condução de calor:

Essa equação também é conhecida como equação de Fourier-Biot e fornece a ferramenta básica para análise de condução de calor. A partir de sua solução, podemos obter o campo de temperatura em função do tempo.

Em palavras, a equação de condução de calor afirma que:

Em qualquer ponto do meio, a taxa líquida de transferência de energia por condução em um volume unitário mais a taxa volumétrica de geração de energia térmica deve ser igual à taxa de variação da energia térmica armazenada dentro do volume.

Veja também: Difusividade térmica

Exemplo – Condução térmica em barra de combustível

A maioria dos PWRs usa o combustível de urânio , que está na forma de dióxido de urânio . O dióxido de urânio é um sólido semicondutor preto com condutividade térmica muito baixa. Por outro lado, o dióxido de urânio tem um ponto de fusão muito alto e um comportamento bem conhecido. A UO ₂ é prensada em pastilhas cilíndricas , essas pastilhas são então sinterizadas no sólido.

Esses pellets cilíndricos são então carregados e encapsulados dentro de uma barra de combustível (ou pino de combustível), feita de ligas de zircônio devido à sua seção transversal de absorção muito baixa (ao contrário do aço inoxidável). A superfície do tubo, que cobre os pellets, é chamada de revestimento de combustível .

Veja também:  Condução térmica de dióxido de urânio

O comportamento térmico e mecânico dos pellets  e barras de combustível constitui uma das três principais disciplinas do projeto. O combustível nuclear é operado sob condições muito inóspitas (térmica, radiação, mecânica) e deve suportar mais do que as condições normais de operação. Por exemplo, as temperaturas no centro dos pellets de combustível atingem mais de 1000 ° C (1832 ° F) acompanhadas por liberações de gás de fissão. Portanto, o conhecimento detalhado da distribuição de temperatura em uma única barra de combustível é essencial para a operação segura do combustível nuclear. Nesta seção, estudaremos a equação de condução de calor em coordenadas cilíndricasusando a condição limite de Dirichlet com determinada temperatura da superfície (ou seja, usando a condição limite de Dirichlet). A análise abrangente do perfil de temperatura da barra de combustível será estudada em seção separada.

Temperatura na linha central de um pellet de combustível

Considere o pellet de combustível com raio r _U = 0,40 cm , no qual há geração uniforme e constante de calor por unidade de volume, q _V [W / m ³ ] . Em vez da taxa de calor volumétrica q _V [W / m ³ ], os engenheiros costumam usar a taxa de calor linear, q _L [W / m] , que representa a taxa de calor de um metro da barra de combustível. A taxa linear de calor pode ser calculada a partir da taxa volumétrica de calor por:

A linha central é tomada como a origem da coordenada r. Devido à simetria na direção z e na direção azimutal, podemos separar as variáveis ​​e simplificar esse problema para um problema unidimensional . Assim, resolveremos apenas a temperatura em função do raio T (r) . Para condutividade térmica constante , k, a forma apropriada da equação de calor cilíndrica é:

A solução geral desta equação é:

onde C ₁ e C ₂ são as constantes de integração.

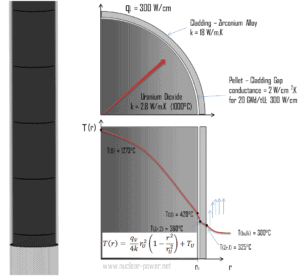
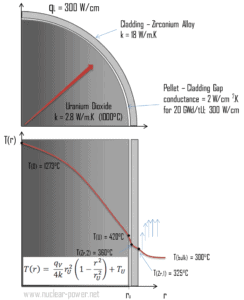Calcule a distribuição de temperatura, T (r) , neste sedimento de combustível, se:

• as temperaturas na superfície do sedimento de combustível são T _U = 420 ° C
• raio da pastilha de combustível r _U = 4 mm .
• a condutividade média do material é k = 2,8 W / mK (corresponde ao dióxido de urânio a 1000 ° C)
• a taxa de calor linear é q _L = 300 W / cm e, portanto, a taxa de calor volumétrica é q _V = 597 x 10 ⁶ W / m ³

Neste caso, a superfície é mantida a temperaturas dadas T _U . Isso corresponde à condição de limite de Dirichlet . Além disso, esse problema é termicamente simétrico e, portanto, também podemos usar a condição de contorno de simetria térmica . As constantes podem ser avaliadas usando a substituição na solução geral e têm a forma:

A distribuição de temperatura resultante e a temperatura da linha central (r = 0) (máxima) neste sedimento cilíndrico de combustível nessas condições de contorno específicas serão:

O fluxo de calor radial em qualquer raio, q _r [Wm ^-1 ], no cilindro pode, é claro, ser determinado usando a distribuição de temperatura e com a lei de Fourier . Observe que, com a geração de calor, o fluxo de calor não é mais independente de r.

∆T no pellet de combustível

O conhecimento detalhado da geometria, raio externo do sedimento de combustível, taxa de calor volumétrico e temperatura da superfície do sedimento (T _U ) determina ∆T entre a superfície externa e a linha central do sedimento de combustível. Portanto, podemos calcular a temperatura da linha central (T _{Zr, 2} ) simplesmente usando a conservação de energia entre o calor gerado no volume e o transferido para fora do volume:

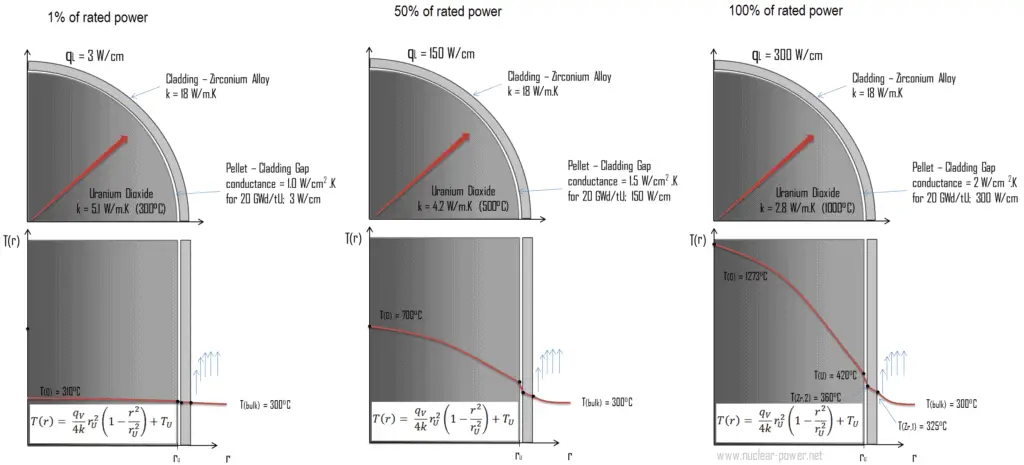
A figura a seguir mostra a distribuição de temperatura no pellet de combustível em vários níveis de potência.

______

A temperatura em um reator operacional varia de ponto a ponto dentro do sistema. Como consequência, há sempre uma vara de combustível e um volume local , que está mais quente  do que todo o resto. Para limitar esses locais quentes, os limites de potência máxima devem ser introduzidos. Os limites de potência máxima estão associados a uma crise de ebulição e às condições que podem causar o derretimento do pellet de combustível. No entanto, considerações metalúrgicas impõem limites superiores à temperatura do revestimento do combustível e do sedimento de combustível. Acima dessas temperaturasexiste o perigo de o combustível ser danificado. Um dos principais objetivos no projeto de reatores nucleares é fornecer a remoção do calor produzido no nível de potência desejado, garantindo que a temperatura máxima do combustível e a temperatura máxima do revestimento estejam sempre abaixo desses valores predeterminados.