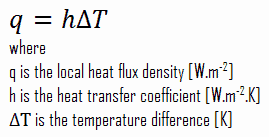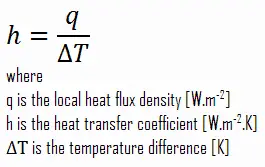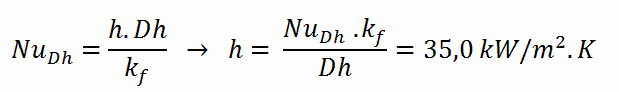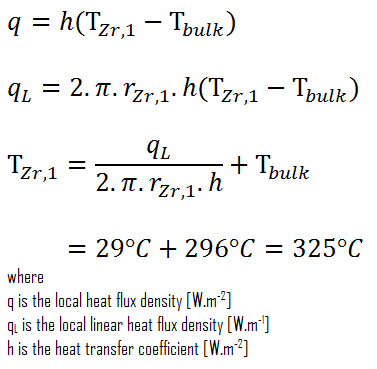Lei do resfriamento de Newton
Apesar da complexidade da convecção , a taxa de transferência de calor por convecção é observada proporcional à diferença de temperatura e é convenientemente expressa pela lei do resfriamento de Newton , que afirma que:
A taxa de perda de calor de um corpo é diretamente proporcional à diferença de temperatura entre o corpo e seus arredores, desde que a diferença de temperatura seja pequena e a natureza da superfície radiante permaneça a mesma.
Observe que ΔT é dado pela temperatura da superfície ou da parede , parede T e temperatura do volume , T ∞ , que é a temperatura do fluido suficientemente longe da superfície.
Coeficiente de transferência de calor por convecção
Como pode ser visto, a constante de proporcionalidade será crucial nos cálculos e é conhecido como coeficiente de transferência de calor por convecção , h . O coeficiente de transferência de calor convectivo, h, pode ser definido como:
A taxa de transferência de calor entre uma superfície sólida e um fluido por unidade de área de superfície por unidade de diferença de temperatura.
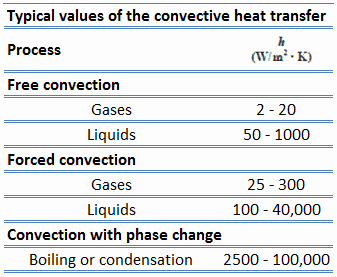 O coeficiente de transferência de calor por convecção depende das propriedades físicas do fluido e da situação física. O coeficiente de transferência de calor por convecção não é uma propriedade do fluido. É um parâmetro determinado experimentalmente, cujo valor depende de todas as variáveis que influenciam a convecção, como a geometria da superfície , a natureza do movimento do fluido , as propriedades do fluido e a velocidade do fluido a granel .
O coeficiente de transferência de calor por convecção depende das propriedades físicas do fluido e da situação física. O coeficiente de transferência de calor por convecção não é uma propriedade do fluido. É um parâmetro determinado experimentalmente, cujo valor depende de todas as variáveis que influenciam a convecção, como a geometria da superfície , a natureza do movimento do fluido , as propriedades do fluido e a velocidade do fluido a granel .
Tipicamente, o coeficiente de transferência de calor por convecção para fluxo laminar é relativamente baixo comparado com o coeficiente de transferência de calor por convecção para fluxo turbulento . Isto é devido ao fluxo turbulento que possui uma camada de filme fluido estagnada mais fina na superfície de transferência de calor.
Deve-se notar que essa camada de filme fluido estagnado desempenha papel crucial para o coeficiente de transferência de calor por convecção. Observa-se que o fluido para completamente na superfície e assume velocidade zero em relação à superfície. Esse fenômeno é conhecido como condição antiderrapante e, portanto, na superfície, o fluxo de energia ocorre puramente por condução. Porém, nas próximas camadas, ocorrem movimentos de condução e difusão-massa no nível molecular ou no nível macroscópico. Devido ao movimento de massa, a taxa de transferência de energia é maior. Como foi escrito, a ebulição nucleadana superfície interrompe efetivamente essa camada estagnada e, portanto, a ebulição nucleada aumenta significativamente a capacidade de uma superfície de transferir energia térmica para o fluido a granel.
Um fenômeno semelhante ocorre para a temperatura. Observa-se que a temperatura do fluido na superfície e na superfície terá a mesma temperatura no ponto de contato. Esse fenômeno é conhecido como condição sem salto de temperatura e é muito importante para a teoria da ebulição de nucleados .
Os valores do coeficiente de transferência de calor , h, foram medidos e tabulados para os fluidos e situações de fluxo comumente encontrados que ocorrem durante a transferência de calor por convecção.
Exemplo: Lei do resfriamento de Newton
 From: Example – Transferência de calor por convecção
From: Example – Transferência de calor por convecção
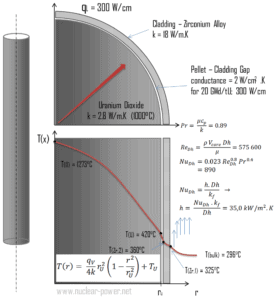
O conhecimento detalhado da geometria, parâmetros do fluido, raio externo do revestimento, taxa de calor linear, coeficiente de transferência de calor por convecção nos permite calcular a diferença de temperatura ∆T entre o líquido de arrefecimento (T a granel ) e a superfície do revestimento (T Zr, 1 ).
Para calcular a temperatura da superfície do revestimento, precisamos saber:
- o diâmetro externo do revestimento é: d = 2 x r Zr, 1 = 9,3 mm
- o número de Nusselt, que é Nu Dh = 890
- o diâmetro hidráulico do canal de combustível é: D h = 13,85 mm
- a condutividade térmica do líquido de refrigeração do reator (300 ° C) é: k H2O = 0,545 W / mK
- a temperatura a granel do líquido de refrigeração do reator nesta coordenada axial é: T a granel = 296 ° C
- a taxa linear de calor do combustível é: q L = 300 W / cm (F Q ≈ 2.0)
O coeficiente de transferência de calor convectivo, h , é dado diretamente pela definição do número de Nusselt:
Finalmente, podemos calcular a temperatura da superfície do revestimento (T Zr, 1 ) simplesmente usando a Lei de Newton de resfriamento :
Para PWRs em operação normal, há água líquida comprimida dentro do núcleo do reator, loops e geradores de vapor. A pressão é mantida em aproximadamente 16MPa . A essa pressão, a água ferve a aproximadamente 350 ° C (662 ° F). Como pode ser visto, a temperatura da superfície T Zr, 1 = 325 ° C garante que mesmo a ebulição sub-resfriada não ocorra. Observe que a ebulição sub-resfriada requer T Zr, 1 = T sat . Como as temperaturas de entrada da água são geralmente de cerca de 290 ° C (554 ° F), é óbvio que este exemplo corresponde à parte inferior do núcleo. Em elevações mais altas do núcleo, a temperatura a granel pode atingir até 330 ° C. A diferença de temperatura de 29 ° C causa a fervura sub-resfriada (330 ° C + 29 ° C> 350 ° C). Por outro lado, a ebulição nucleada na superfície interrompe efetivamente a camada estagnada e, portanto, a ebulição nucleada aumenta significativamente a capacidade de uma superfície de transferir energia térmica para o fluido a granel. Como resultado, o coeficiente de transferência de calor por convecção aumenta significativamente e, portanto, em elevações mais altas, a diferença de temperatura (T Zr, volume 1 – T ) diminui significativamente.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.