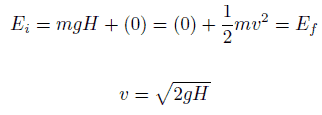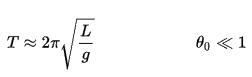O que é exemplo de energia cinética – definição

O que é energia cinética

A energia cinética, K , é definida como a energia armazenada em um objeto por causa de seu movimento. Um objeto em movimento tem a capacidade de fazer o trabalho e, portanto, pode-se dizer que possui energia. É chamado de energia cinética, da palavra grega kinetikos, que significa “movimento”.

A energia cinética depende da velocidade de um objeto e é a capacidade de um objeto em movimento de trabalhar em outros objetos quando colide com eles. Por outro lado, a energia cinética de um objeto representa a quantidade de energia necessária para aumentar a velocidade do objeto do repouso (v = 0) para sua velocidade final. A energia cinética também depende linearmente da massa, que é uma medida numérica da inércia do objeto e a medida da resistência de um objeto à aceleração quando uma força é aplicada.

Definimos a quantidade:

K = ½ mv ²

ser a energia cinética translacional do objeto. É preciso acrescentar que é chamada energia cinética “translacional” para distingui-la da energia cinética rotacional.

Bloco deslizando por uma ladeira sem atrito

O bloco de 1 kg inicia uma altura H (digamos 1 m) acima do solo, com energia potencial mgH e energia cinética igual a 0. Desliza para o chão (sem atrito) e chega sem energia potencial e energia cinética K = ½ mv ² . Calcule a velocidade do bloco no chão e sua energia cinética.

E _mech = U + K = const

=> ½ mv ² = mgH

=> v = √2gH = 4,43 m / s

=> K ₂ = ½ x 1 kg x (4,43 m / s) ² = 19,62 kg.m ² .s ^-2 = 19,62 J

Pêndulo

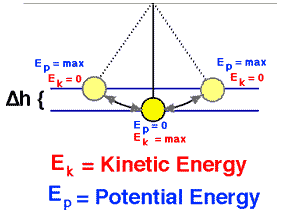Suponha um pêndulo (bola de massa m suspensa em uma corda de comprimento L que têm puxado para cima de modo a que a bola é uma altura H <G acima do seu ponto mais baixo do arco do seu movimento corda esticada. O pêndulo é submetido ao conservador força gravitacional, onde forças de atrito como o arrasto aéreo e o atrito no pivô são desprezíveis.

Nós o liberamos do descanso. Quão rápido está indo no fundo?

O pêndulo atinge a maior energia cinética e menos energia potencial quando na posição vertical , porque terá a maior velocidade e estará mais próximo da Terra neste ponto. Por outro lado, terá sua energia menos cinética e maior energia potencial nas posições extremas de seu balanço, porque possui velocidade zero e está mais distante da Terra nesses pontos.

Se a amplitude é limitada a pequenas oscilações, o período T de um pêndulo simples, o tempo necessário para um ciclo completo, é:

onde L é o comprimento do pêndulo eg é a aceleração local da gravidade. Para balanços pequenos, o período de oscilação é aproximadamente o mesmo para balanços de tamanhos diferentes. Ou seja,  o período é independente da amplitude .

Exemplo: energia cinética do próton

Um próton ( m = 1,67 x ^10-27 kg ) viaja a uma velocidade v = 0,9900c = 2,968 x 10 ⁸ m / s . Qual é a sua energia cinética ?

De acordo com um cálculo clássico, que não está correto, obteríamos:

K = 1 / 2mv ² = ½ x (1,67 x ^10-27 kg) x (2,968 x 10 ⁸ m / s) ² = 7,355 x 10 ^-11 J

Com a correção relativística, a energia cinética relativística é igual a:

K = (ɣ – 1) mc ²

onde o fator de Lorentz

ɣ = 7.089

Portanto

K = 6,089 x (1,67 x 10 ^-27 kg) x (2,9979 x 10 ⁸ m / s) ² = 9,139 x ^10-10 J = 5,701 GeV

Isso é cerca de 12 vezes mais energia do que no cálculo clássico. De acordo com essa relação, a aceleração de um feixe de prótons para 5,7 GeV requer energias da ordem diferente.