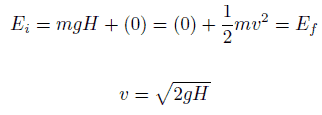Was ist kinetische Energie?
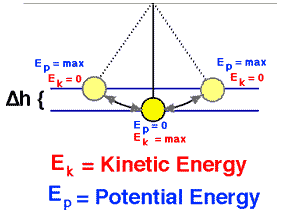
Die kinetische Energie K ist definiert als die Energie, die aufgrund ihrer Bewegung in einem Objekt gespeichert ist. Ein in Bewegung befindliches Objekt hat die Fähigkeit zu arbeiten und kann somit als energiereich bezeichnet werden. Es wird kinetische Energie genannt, vom griechischen Wort kinetikos, was “Bewegung” bedeutet.
Die kinetische Energie hängt von der Geschwindigkeit eines Objekts ab und ist die Fähigkeit eines sich bewegenden Objekts, an anderen Objekten zu arbeiten, wenn es mit ihnen kollidiert. Andererseits stellt die kinetische Energie eines Objekts die Energiemenge dar, die erforderlich ist, um die Geschwindigkeit des Objekts aus dem Ruhezustand (v = 0) auf seine Endgeschwindigkeit zu erhöhen. Die kinetische Energie hängt auch linear von der Masse ab, die ein numerisches Maß für die Trägheit des Objekts und das Maß für den Widerstand eines Objekts gegen die Beschleunigung ist, wenn eine Kraft ausgeübt wird.
Wir definieren die Menge:
K = 1/2 mv 2
die translatorische kinetische Energie des Objekts zu sein. Es muss hinzugefügt werden, es wird die “translatorische” kinetische Energie genannt, um es von der kinetischen Rotationsenergie zu unterscheiden.
Beispiele für kinetische Energie
- Kinetische Energie von Spaltfragmenten
- Kinetische Energie von sofortigen Neutronen
Block rutschen eine reibungslose Steigung hinunter
Der 1-kg-Block beginnt eine Höhe H (sagen wir 1 m) über dem Boden mit einer potentiellen Energie mgH und einer kinetischen Energie von 0. Er gleitet auf den Boden (ohne Reibung) und kommt ohne potentielle Energie und kinetische Energie an K = ½ mv 2 . Berechnen Sie die Geschwindigkeit des Blocks am Boden und seine kinetische Energie.
E mech = U + K = const
=> ½ mv 2 = mgH
=> v = √2gH = 4,43 m / s
=> K 2 = ½ x 1 kg x (4,43 m / s) 2 = 19,62 kg.m 2 .s -2 = 19,62 J
Pendel
Nehmen Sie ein Pendel an (Kugel der Masse m, die an einer Schnur der Länge L aufgehängt ist , die wir hochgezogen haben, so dass die Kugel eine Höhe H <L über ihrem tiefsten Punkt im Bogen ihrer Bewegung der gedehnten Schnur liegt. Das Pendel wird dem Konservativen unterworfen Gravitationskraft, bei der Reibungskräfte wie Luftwiderstand und Reibung am Drehpunkt vernachlässigbar sind.
Wir befreien es von der Ruhe. Wie schnell geht es unten?
Das Pendel erreicht in vertikaler Position die größte kinetische Energie und die geringste potentielle Energie , da es die größte Geschwindigkeit hat und an diesem Punkt der Erde am nächsten ist. Andererseits hat es an den extremen Positionen seines Schwungs seine geringste kinetische Energie und seine größte potentielle Energie , da es keine Geschwindigkeit hat und an diesen Punkten am weitesten von der Erde entfernt ist.
Wenn die Amplitude auf kleine Schwankungen begrenzt ist, beträgt die Periode T eines einfachen Pendels, die Zeit, die für einen vollständigen Zyklus benötigt wird:
Dabei ist L die Länge des Pendels und g die lokale Erdbeschleunigung. Bei kleinen Schaukeln ist die Schwungdauer für Schaukeln unterschiedlicher Größe ungefähr gleich. Das heißt, die Periode ist unabhängig von der Amplitude .
Beispiel: Protons kinetische Energie
Ein Proton ( m = 1,67 × 10 –27 kg ) bewegt sich mit einer Geschwindigkeit v = 0,9900 c = 2,968 × 10 8 m / s . Was ist seine kinetische Energie ?
Nach einer klassischen Berechnung, die nicht korrekt ist, würden wir erhalten:
K = 1 / 2mv 2 = ½ x (1,67 x 10 -27 kg) x (2,968 x 10 8 m / s) 2 = 7,355 x 10 -11 J.
Bei der relativistischen Korrektur ist die relativistische kinetische Energie gleich:
K = (ɣ – 1) mc 2
wo der Lorentz-Faktor
ɣ = 7,089
deshalb
K = 6,089 × (1,67 × 10 –27 kg) × (2,9979 × 10 8 m / s) 2 = 9,139 × 10 –10 J = 5,701 GeV
Dies ist etwa 12-mal höhere Energie als bei der klassischen Berechnung. Entsprechend dieser Beziehung erfordert eine Beschleunigung eines Protonenstrahls auf 5,7 GeV Energien, die in der Größenordnung unterschiedlich sind.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
