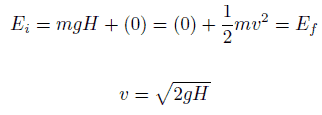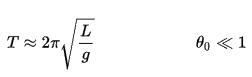Quelle est l’énergie cinétique
L’énergie cinétique, K , est définie comme l’énergie stockée dans un objet en raison de son mouvement. Un objet en mouvement a la capacité de travailler et peut donc être considéré comme ayant de l’énergie. Cela s’appelle l’énergie cinétique, du mot grec kinetikos, qui signifie «mouvement».
L’ énergie cinétique dépend de la vitesse d’un objet et correspond à la capacité d’un objet en mouvement à travailler sur d’autres objets lorsqu’il entre en collision avec eux. D’autre part, l’énergie cinétique d’un objet représente la quantité d’énergie nécessaire pour augmenter la vitesse de l’objet du repos (v = 0) à sa vitesse finale. L’énergie cinétique dépend également de manière linéaire de la masse, qui est une mesure numérique de l’ inertie de l’objet et la mesure de la résistance de celui-ci à l’accélération lorsqu’une force est appliquée.
Nous définissons la quantité:
K = ½ mv 2
être l’ énergie cinétique de translation de l’objet. Il faut ajouter qu’on l’appelle énergie cinétique «translationnelle» pour la distinguer de l’énergie cinétique rotationnelle.
Exemples d’énergie cinétique
Bloc glissant sur une pente inclinée sans friction
Le bloc de 1 kg commence à une hauteur H (disons 1 m) au-dessus du sol, avec une énergie potentielle mgH et une énergie cinétique égale à 0. Il glisse vers le sol (sans frottement) et arrive sans énergie potentielle et énergie cinétique K = ½ mv 2 . Calculez la vitesse du bloc au sol et son énergie cinétique.
E mech = U + K = const
=> ½ mv 2 = mgH
=> v = √2gH = 4,43 m / s
=> K 2 = ½ x 1 kg x (4,43 m / s) 2 = 19,62 kg.m 2 .s -2 = 19,62 J
Pendule
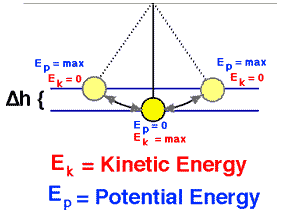 Supposons un pendule (boule de masse m suspendue à une chaîne de longueur L que nous avons tirée de sorte que la balle soit à une hauteur H <L au-dessus de son point le plus bas sur l’arc de son mouvement de corde tendue. Le pendule est soumis au conservateur force gravitationnelle où les forces de friction comme la traînée d’air et la friction au pivot sont négligeables.
Supposons un pendule (boule de masse m suspendue à une chaîne de longueur L que nous avons tirée de sorte que la balle soit à une hauteur H <L au-dessus de son point le plus bas sur l’arc de son mouvement de corde tendue. Le pendule est soumis au conservateur force gravitationnelle où les forces de friction comme la traînée d’air et la friction au pivot sont négligeables.
Nous le libérons du repos. À quelle vitesse va-t-il au fond?
Le pendule atteint la plus grande énergie cinétique et le moins d’énergie potentielle lorsqu’il est en position verticale , car il aura la plus grande vitesse et sera le plus proche de la Terre à ce point. D’un autre côté, il aura sa moindre énergie cinétique et sa plus grande énergie potentielle aux positions extrêmes de son swing, car il a une vitesse nulle et est le plus éloigné de la Terre en ces points.
Si l’amplitude est limitée à de petites oscillations, la période T d’un simple pendule, le temps pris pour un cycle complet, est:
où L est la longueur du pendule et g est l’accélération locale de la gravité. Pour les petites balançoires, la période de balancement est approximativement la même pour les balançoires de tailles différentes. Autrement dit, la période est indépendante de l’amplitude .
Exemple: énergie cinétique du proton
 Un proton ( m = 1,67 x 10 -27 kg ) se déplace à une vitesse v = 0,9900c = 2,968 x 10 8 m / s . Quelle est son énergie cinétique ?
Un proton ( m = 1,67 x 10 -27 kg ) se déplace à une vitesse v = 0,9900c = 2,968 x 10 8 m / s . Quelle est son énergie cinétique ?
Selon un calcul classique, qui n’est pas correct, on obtiendrait:
K = 1 / 2mv 2 = ½ x (1,67 x 10 -27 kg) x (2,968 x 10 8 m / s) 2 = 7,355 x 10 -11 J
Avec la correction relativiste, l’énergie cinétique relativiste est égale à:
K = (ɣ – 1) mc 2
où le facteur de Lorentz
ɣ = 7,089
par conséquent
K = 6,089 x (1,67 x 10 -27 kg) x (2,9979 x 10 8 m / s) 2 = 9,139 x 10 -10 J = 5,701 GeV
C’est environ 12 fois plus d’ énergie que dans le calcul classique. Selon cette relation, une accélération d’un faisceau de protons à 5,7 GeV nécessite des énergies qui sont dans l’ordre différent.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci