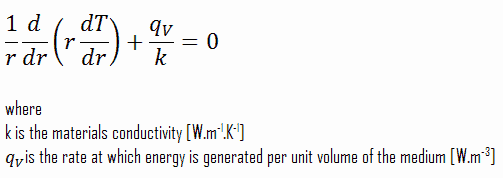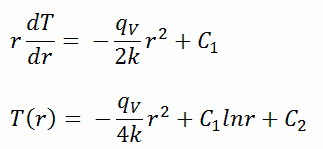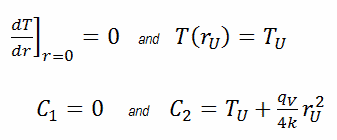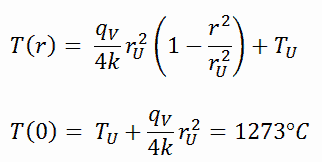Geração de calor em reatores nucleares
Como foi escrito, uma usina nuclear ( usina nuclear) parece uma usina termelétrica padrão, com uma exceção. A fonte de calor na usina nuclear é um reator nuclear . Como é típico em todas as centrais térmicas convencionais, o calor é usado para gerar vapor que aciona uma turbina a vapor conectada a um gerador que produz eletricidade. Mas em usinas nucleares, os reatores produzem uma quantidade enorme de calor (energia) em um pequeno volume . A densidade da geração de energia é muito grande e isso exige muito do seu sistema de transferência de calor (sistema de refrigeração do reator).
Para que um reator opere em estado estacionário, todo o calor liberado no sistema deve ser removido tão rápido quanto produzido . Isso é feito passando um líquido refrigerante líquido ou gasoso pelo núcleo e por outras regiões onde o calor é gerado. A transferência de calor deve ser igual ou superior à taxa de geração de calor ou superaquecimento, podendo ocorrer danos ao combustível. A natureza e operação deste sistema de refrigeração é uma das considerações mais importantes no projeto de um reator nuclear.
Deve-se notar que, do ponto de vista estritamente nuclear, teoricamente não há limite superior à energia térmica do reator, que pode ser atingida por qualquer reator crítico com excesso de reatividade suficiente para superar seus feedbacks negativos de temperatura. Em cada reator nuclear , há uma proporcionalidade direta entre o fluxo de nêutrons e a energia térmica do reator . O termo energia térmica é geralmente usado, porque significa a taxa na qual o calor é produzido no núcleo do reator como resultado de fissões no combustível. Além disso, por um curto período, um reator crítico não precisa ter alto excesso de reatividade, como no caso de excursões rápidas de reatividade.
Em resumo, quase todo reator é capaz de exceder a capacidade de remoção de calor de seu sistema de refrigeração. Além deste ponto, o combustível aqueceria e poderá atingir temperaturas muito altas. Essa situação deve ser evitada pelo operador do reator e pelos sistemas de segurança do reator. É essencial que o equilíbrio da taxa de geração de calor e remoção de calor seja mantido para evitar essas temperaturas que podem resultar em falha de combustível ou outros materiais estruturais. Na engenharia de reatores, o sistema hidráulico térmico dos reatores nucleares descreve o esforço que envolve o acoplamento da transferência de calor e da dinâmica de fluidos para atingir a taxa de remoção de calor desejada do núcleo, tanto em condições normais de operação quanto em acidentes.
Produção de calor em elementos combustíveis
Nos reatores nucleares , há uma proporcionalidade direta entre o fluxo de nêutronse a energia térmica do reator . Essa proporcionalidade é determinada pela taxa de reação de fissão por unidade de volume ( RR = Ф. Σ ). A taxa de reação de fissão dentro de um reator nuclear é controlada por vários fatores. Por simplicidade, suponha que o material fissionável esteja uniformemente distribuído no reator. Neste caso, as seções macroscópicas são independentes da posição. Multiplicando a taxa de reação de fissão por unidade de volume ( RR = Ф. Σ ) pelo volume totaldo núcleo (V) nos fornece o número total de reações que ocorrem no núcleo do reator por unidade de tempo. Mas também sabemos que a quantidade de energia liberada por uma reação de fissão é de cerca de 200 MeV / fissão . Agora, é possível determinar a taxa de liberação de energia (potência) devido à reação de fissão. É dado pela seguinte equação:
P = RR. E r . V = Ф. Σ f . E r . V = Ф. N U235 . σ f 235 . E r . V
Onde:
P – potência do reator (MeV.s -1 )
Ф – fluxo de nêutrons (nêutrons.cm -2 .s -1 )
σ – seção microscópica (cm 2 )
N – densidade numérica atômica (atoms.cm -3 )
Er – a energia recuperável média por fissão (MeV / fissão)
V – volume total do núcleo (m 3 )
Em geral, a fissão nuclear resulta na liberação de enormes quantidades de energia . A quantidade de energia depende fortemente do núcleo a ser fissionado e também depende fortemente da energia cinética de um nêutron incidente . Para calcular a potência de um reator, é necessário ser capaz de identificar com precisão os componentes individuais dessa energia . A princípio, é importante distinguir entre a energia total liberada e a energia que pode ser recuperada em um reator .
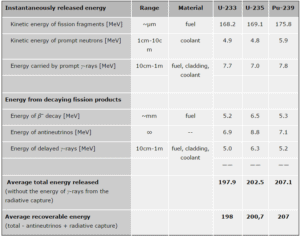A energia total liberada na fissão pode ser calculada a partir das energias de ligação do núcleo alvo inicial a serem fissionadas e das energias de ligação dos produtos de fissão . Mas nem toda a energia total pode ser recuperada em um reator. Por exemplo, cerca de 10 MeV são liberados na forma de neutrinos (na verdade antineutrinos ). Como os neutrinos estão interagindo fracamente (com seção transversal extremamente baixa de qualquer interação), eles não contribuem para a energia que pode ser recuperada em um reator.
Como pode ser visto na tabela, a energia total liberada em um reator é de cerca de 210 MeV por fissão de 235 U , distribuída conforme mostrado na tabela. Em um reator, a energia recuperável média por fissão é de cerca de 200 MeV , sendo a energia total menos a energia da energia dos antineutrinos que são irradiados. Isto significa que cerca de 3,1 ⋅ 10 10 fissões por segundo são necessárias para produzir uma potência de 1 W . Como 1 grama de qualquer material físsil contém cerca de 2,5 x 10 21 núcleos, a fissão de 1 grama de material físsil produz cerca de 1 megawatt-dia (MWd) de energia térmica.
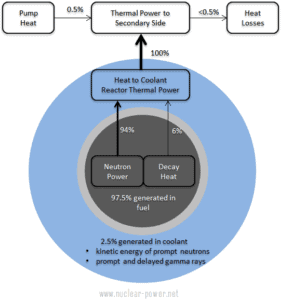
Como pode ser visto na descrição dos componentes individuais da energia total liberada durante a reação de fissão, há uma quantidade significativa de energia gerada fora do combustível nuclear (barras de combustível externas). Especialmente a energia cinética dos nêutrons imediatos é amplamente gerada no refrigerante ( moderador ) . Esse fenômeno precisa ser incluído nos cálculos nucleares.
Para LWR , é geralmente aceito que cerca de 2,5% da energia total é recuperada no moderador . Essa fração de energia depende dos materiais, sua disposição dentro do reator e, portanto, do tipo de reator.
Também deve ser adicionado, também os outros internos do reator devem ser resfriados o suficiente para evitar o superaquecimento de seus materiais de construção. Um dos componentes mais expostos é o refletor de nêutrons , especialmente o refletor pesado. Enquanto atua como um escudo de nêutrons, o refletor pesado é aquecido devido à absorção da radiação gama . Para evitar superaquecimento, o calor no refletor é removido pela água que flui através dos canais de resfriamento perfurados no refletor.
Veja também: Liberação de energia por fissão
Veja também: Calor residual
Distribuição de energia em núcleos de reatores convencionais
Deve-se notar que a forma do fluxo derivada da teoria da difusão é apenas um caso teórico em um reator cilíndrico homogêneo uniforme em baixos níveis de potência (com “ criticidade zero de potência ”). Assumimos implicitamente que o núcleo constituído por milhares de elementos de combustível e controle, refrigerante e estrutura pode ser representado por alguma mistura homogênea eficaz. Essa é uma suposição muito forte , porque não leva em conta a heterogeneidade de um núcleo.
Veja também: Equação de difusão – Reator cilíndrico finito
Nos núcleos de reatores comerciais, a distribuição do fluxo é significativamente influenciada por muitos fatores. Um dos aspectos mais importantes é a heterogeneidade da montagem do moderador de combustível. Esse problema é muito complexo e é descrito separadamente em:
Veja também: Distribuição de energia
Limites térmicos
A temperatura em um reator operacional varia de ponto a ponto dentro do sistema. Como consequência, há sempre uma vara de combustível e um volume local , que está mais quente do que todo o resto. Para limitar esses locais quentes, os limites de potência máxima devem ser introduzidos. Os limites de potência de pico estão associados a fenômenos como a partida da ebulição nucleada e às condições que podem causar o derretimento do pellet de combustível.
Portanto, a distribuição de energia dentro do núcleo deve ser adequadamente limitada. Essas limitações são geralmente divididas em duas categorias básicas:
- Limitação da distribuição global de energia
- Limitação da distribuição de energia local
Delta do líquido refrigerante do reator T – Balanço de energia
Outra relação muito útil é que a energia térmica produzida por um reator está diretamente relacionada à vazão mássica do líquido de arrefecimento do reator e à diferença de temperatura através do núcleo.
Numa base termodinâmica direta, essa geração de calor também está relacionada à diferença de temperatura do fluido através do núcleo e à taxa de fluxo de massa do fluido que passa através do núcleo. Assim, o tamanho do núcleo do reator é dependente e limitado por muito pouco líquido pode ser passado através do núcleo para remover a energia térmica gerada . Observe que, em PWRs , a temperatura de saída do núcleo é limitada. Em um reator de água pressurizada típico, o líquido de arrefecimento primário quente ( água 330 ° C; 626 ° F ) é bombeado para o gerador de vaporatravés da entrada primária. Isso requer manutenção de pressões muito altas para manter a água no estado líquido. Para impedir a ebulição do líquido de arrefecimento primário e fornecer uma margem de sub-resfriamento (a diferença entre a temperatura do pressurizador e a temperatura mais alta no núcleo do reator), pressões em torno de 16 MPa são típicas para PWRs . O vaso de pressão do reator é o componente principal, que limita a eficiência térmica de cada usina nuclear , uma vez que o vaso do reator deve suportar altas pressões. Muitos outros fatores afetam a quantidade de calor gerada dentro do núcleo de um reator, mas sua taxa de geração limitante é baseada na quantidade de energia que pode ser transportada com segurança pelo refrigerante.
Perfil de temperatura – combustível nuclear
Veja também: Temperatura da superfície do revestimento
A maioria dos PWRs usa o combustível de urânio , que está na forma de dióxido de urânio . O dióxido de urânio é um sólido semicondutor preto com condutividade térmica muito baixa. Por outro lado, o dióxido de urânio tem um ponto de fusão muito alto e um comportamento bem conhecido. A UO 2 é prensada em pastilhas cilíndricas , essas pastilhas são então sinterizadas no sólido.
Essas pastilhas cilíndricas são então carregadas e encapsuladas dentro de uma barra de combustível (ou pino de combustível), que é feita de ligas de zircônio devido à sua seção transversal de absorção muito baixa (ao contrário do aço inoxidável). A superfície do tubo, que cobre os pellets, é chamada de revestimento de combustível .
Veja também: Condução térmica de dióxido de urânio
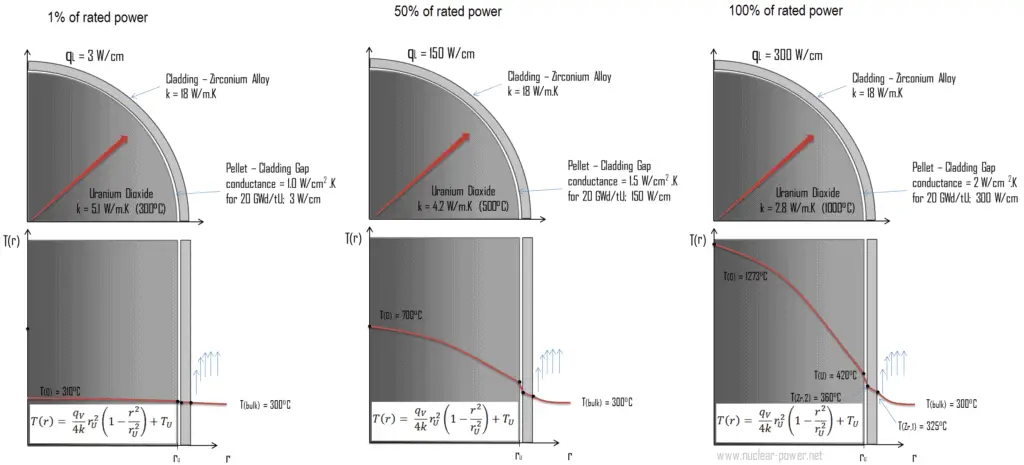
O comportamento térmico e mecânico dos pellets e barras de combustível constitui uma das três principais disciplinas do projeto. O combustível nuclear é operado sob condições muito inóspitas (térmica, radiação, mecânica) e deve suportar mais do que as condições normais de operação. Por exemplo, as temperaturas no centro dos pellets de combustível atingem mais de 1000 ° C (1832 ° F) acompanhadas por liberações de gás de fissão. Portanto, o conhecimento detalhado da distribuição de temperatura em uma única barra de combustível é essencial para a operação segura do combustível nuclear. Nesta seção, estudaremos a equação de condução de calor em coordenadas cilíndricasusando a condição limite de Dirichlet com determinada temperatura da superfície (ou seja, usando a condição limite de Dirichlet). A análise abrangente do perfil de temperatura da barra de combustível será estudada em seção separada.
Temperatura na linha central de um pellet de combustível
Considere o pellet de combustível com raio r U = 0,40 cm , no qual há geração uniforme e constante de calor por unidade de volume, q V [W / m 3 ] . Em vez da taxa de calor volumétrica q V [W / m 3 ], os engenheiros costumam usar a taxa de calor linear, q L [W / m] , que representa a taxa de calor de um metro da barra de combustível. A taxa linear de calor pode ser calculada a partir da taxa volumétrica de calor por:
A linha central é tomada como a origem da coordenada r. Devido à simetria na direção z e na direção azimutal, podemos separar as variáveis e simplificar esse problema para um problema unidimensional . Assim, resolveremos apenas a temperatura em função do raio T (r) . Para condutividade térmica constante , k, a forma apropriada da equação de calor cilíndrica é:
A solução geral desta equação é:
onde C 1 e C 2 são as constantes de integração.
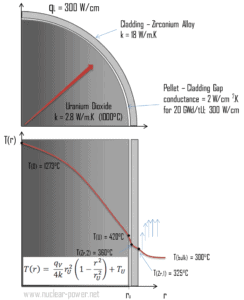Calcule a distribuição de temperatura, T (r) , neste sedimento de combustível, se:
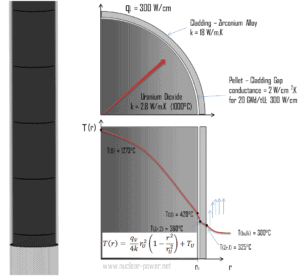
- as temperaturas na superfície do sedimento de combustível são T U = 420 ° C
- raio da pastilha de combustível r U = 4 mm .
- a condutividade média do material é k = 2,8 W / mK (corresponde ao dióxido de urânio a 1000 ° C)
- a taxa de calor linear é q L = 300 W / cm e, portanto, a taxa de calor volumétrica é q V = 597 x 10 6 W / m 3
Neste caso, a superfície é mantida a temperaturas dadas T U . Isso corresponde à condição de limite de Dirichlet . Além disso, esse problema é termicamente simétrico e, portanto, também podemos usar a condição de contorno de simetria térmica . As constantes podem ser avaliadas usando a substituição na solução geral e têm a forma:
A distribuição de temperatura resultante e a temperatura da linha central (r = 0) (máxima) neste sedimento cilíndrico de combustível nessas condições de contorno específicas serão:
O fluxo de calor radial em qualquer raio, q r [Wm -1 ], no cilindro pode, é claro, ser determinado usando a distribuição de temperatura e com a lei de Fourier . Observe que, com a geração de calor, o fluxo de calor não é mais independente de r.
A figura a seguir mostra a distribuição de temperatura no pellet de combustível em vários níveis de potência.
______
A temperatura em um reator operacional varia de ponto a ponto dentro do sistema. Como consequência, há sempre uma vara de combustível e um volume local , que está mais quente do que todo o resto. Para limitar esses locais quentes, os limites de potência máxima devem ser introduzidos. Os limites de potência máxima estão associados a uma crise de ebulição e às condições que podem causar o derretimento do pellet de combustível. No entanto, considerações metalúrgicas impõem limites superiores à temperatura do revestimento do combustível e do sedimento de combustível. Acima dessas temperaturasexiste o perigo de o combustível ser danificado. Um dos principais objetivos no projeto de reatores nucleares é fornecer a remoção do calor produzido no nível de potência desejado, garantindo que a temperatura máxima do combustível e a temperatura máxima do revestimento estejam sempre abaixo desses valores predeterminados.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
