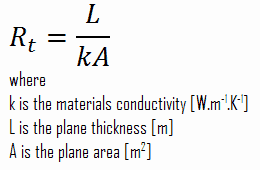Lei de Fourier de condução térmica
Os processos de transferência de calor podem ser quantificados em termos de equações de taxa apropriadas. A equação da taxa neste modo de transferência de calor é baseada na lei de condução térmica de Fourier . Esta lei estabelece que a taxa de tempo de transferência de calor através de um material é proporcional ao gradiente negativo na temperatura e à área, perpendicularmente àquele gradiente, através do qual o calor flui. Sua forma diferencial é:
A constante de proporcionalidade obtida na relação é conhecida como condutividade térmica , k (ou λ ), do material. Um material que transfere energia prontamente por condução é um bom condutor térmico e possui um alto valor de k . A lei de Fourier é uma expressão que define a condutividade térmica .Como pode ser visto, para resolver a lei de Fourier , precisamos envolver a diferença de temperatura, a geometria e a condutividade térmica do objeto. Essa lei foi formulada pela primeira vez por Joseph Fourier em 1822, que concluiu que “o fluxo de calor resultante da condução térmica é proporcional à magnitude do gradiente de temperatura e oposto ao sinal”.
Da mesma forma, como a lei de Fourier determina o fluxo de calor através de uma laje, ela também pode ser usada para determinar a diferença de temperatura, quando q é conhecido. Isso pode ser usado para o cálculo da temperatura no centro do pellet de combustível, como será mostrado nas seções a seguir.
Exemplo – Fluxo de calor através de uma janela
Perda de calor através das janelas
Uma das principais fontes de perda de calor de uma casa é através das janelas. Calcule a taxa de fluxo de calor através de uma janela de vidro com 1,5 mx 1,0 m de área e 3,0 mm de espessura, se as temperaturas nas superfícies interna e externa forem de 14,0 ° C e 13,0 ° C, respectivamente. Calcule o fluxo de calor através desta janela.
Solução:
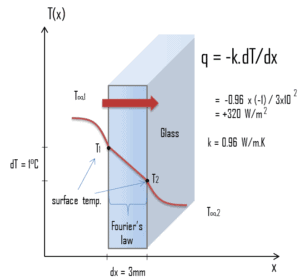
Neste ponto, conhecemos as temperaturas nas superfícies do material. Essas temperaturas são dadas também pelas condições dentro e fora da casa. Nesse caso, o calor flui por condução através do vidro da temperatura interna mais alta para a temperatura externa mais baixa. Usamos a lei de Fourier da equação de condução térmica:
Assumimos que a condutividade térmica de um vidro comum é k = 0,96 W / mK
O fluxo de calor será então:
q = 0,96 [W / mK] x 1 [K] / 3,0 x 10 -3 [m] = 320 W / m 2
A perda total de calor através desta janela será:
q perda = q. A = 320 x 1,5 x 1,0 = 480W
Lei de Fourier e resistência térmica
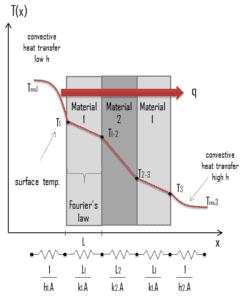A resistência térmica é o inverso da condutância térmica. Assim como uma resistência elétrica está associada à condução de eletricidade, uma resistência térmica pode estar associada à condução de calor.
Considere uma parede plana de espessura L e condutividade térmica média k. As duas superfícies da parede são mantidos a temperaturas constantes de T 1 e T 2 . Para condução de calor constante unidimensional através da parede, temos T (x). Então a lei de Fourier de condução de calor para a parede pode ser expressa como:
A resistência térmica é uma propriedade de calor e uma medição de uma diferença de temperatura pela qual um objeto ou material resiste ao fluxo de calor. A resistência térmica para condução em uma parede plana é definida como:
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
