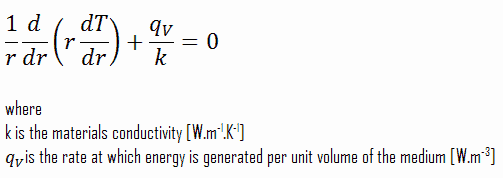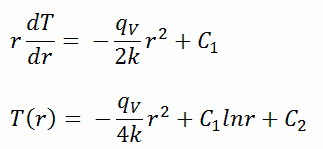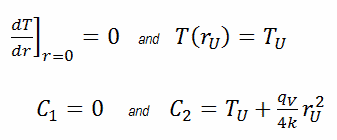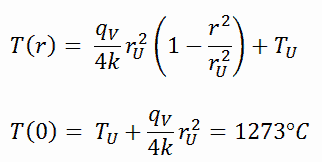Temperaturprofil – Kernbrennstoff
Siehe auch: Wärmeerzeugung in Kernreaktoren
Siehe auch: Manteloberflächentemperatur
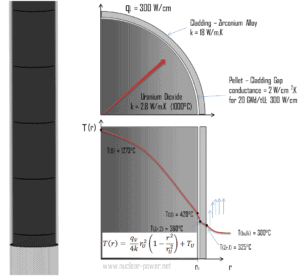
Die meisten DWR verwenden den Uranbrennstoff , der in Form von Urandioxid vorliegt . Urandioxid ist ein schwarzer halbleitender Feststoff mit sehr geringer Wärmeleitfähigkeit. Andererseits hat das Urandioxid einen sehr hohen Schmelzpunkt und ein bekanntes Verhalten. Das UO 2 wird zu zylindrischen Pellets gepresst , diese Pellets werden dann zu dem Feststoff gesintert.
Diese zylindrischen Pellets werden dann in einem Brennstab (oder Brennstoff pin) geladen und eingekapselt, die aus Zirconium – Legierungen sind aufgrund seines sehr geringen Absorptionsquerschnittes (im Unterschied zu dem rostfreien Stahl). Die Oberfläche des Rohrs, die die Pellets bedeckt, wird als Brennstoffhülle bezeichnet .
Siehe auch: Wärmeleitung von Urandioxid
Das thermische und mechanische Verhalten von Brennstoffpellets und Brennstäben ist eine der drei Hauptdisziplinen des Entwurfs. Kernbrennstoff wird unter sehr unwirtlichen Bedingungen (Wärme, Strahlung, mechanisch) betrieben und muss mehr als normalen Betriebsbedingungen standhalten. Beispielsweise erreichen die Temperaturen im Zentrum von Brennstoffpellets mehr als 1000 ° C (1832 ° F), begleitet von Spaltgasfreisetzungen. Daher ist eine detaillierte Kenntnis der Temperaturverteilung innerhalb eines einzelnen Brennstabs für den sicheren Betrieb von Kernbrennstoffen unerlässlich. In diesem Abschnitt werden wir die Wärmeleitungsgleichung in Zylinderkoordinaten untersuchenunter Verwendung der Dirichlet-Randbedingung bei gegebener Oberflächentemperatur (dh unter Verwendung der Dirichlet-Randbedingung). Eine umfassende Analyse des Brennstabtemperaturprofils wird in einem separaten Abschnitt untersucht.
Temperatur in der Mittellinie eines Brennstoffpellets
Betrachten Sie das Brennstoffpellet mit dem Radius r U = 0,40 cm , bei dem pro Volumeneinheit eine gleichmäßige und konstante Wärmeentwicklung q V [W / m 3 ] auftritt . Anstelle der volumetrischen Heizrate q V [W / m 3 ] verwenden Ingenieure häufig die lineare Heizrate q L [W / m] , die die Heizrate eines Meters Brennstab darstellt. Die lineare Heizrate kann aus der volumetrischen Heizrate berechnet werden durch:
Die Mittellinie wird als Ursprung für die r-Koordinate verwendet. Aufgrund der Symmetrie in z-Richtung und in azimutaler Richtung können wir Variablen trennen und dieses Problem zu einem eindimensionalen Problem vereinfachen . Wir lösen also nur die Temperatur als Funktion des Radius T (r) . Für eine konstante Wärmeleitfähigkeit ist k die geeignete Form der zylindrischen Wärmegleichung :
Die allgemeine Lösung dieser Gleichung lautet:
wobei C 1 und C 2 die Integrationskonstanten sind.
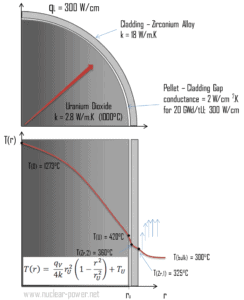 Berechnen Sie die Temperaturverteilung T (r) in diesem Brennstoffpellet, wenn:
Berechnen Sie die Temperaturverteilung T (r) in diesem Brennstoffpellet, wenn:
- Die Temperaturen an der Oberfläche des Brennstoffpellets betragen T U = 420 ° C.
- der Brennstoffpelletradius r U = 4 mm .
- Die Leitfähigkeit des gemittelten Materials beträgt k = 2,8 W / mK (entspricht Urandioxid bei 1000 ° C).
- Die lineare Heizrate beträgt q L = 300 W / cm und somit beträgt die volumetrische Heizrate q V = 597 × 10 6 W / m 3
In diesem Fall wird die Oberfläche bei gegebenen Temperaturen T U gehalten . Dies entspricht der Dirichlet-Randbedingung . Darüber hinaus ist dieses Problem thermisch symmetrisch und daher können wir auch die thermische Symmetrie-Randbedingung verwenden . Die Konstanten können durch Substitution in die allgemeine Lösung bewertet werden und haben die Form:
Die resultierende Temperaturverteilung und die Mittellinientemperatur (r = 0) (maximal) in diesem zylindrischen Brennstoffpellet bei diesen spezifischen Randbedingungen sind:
Der radiale Wärmefluss bei jedem Radius q r [Wm -1 ] im Zylinder kann natürlich unter Verwendung der Temperaturverteilung und nach dem Fourier-Gesetz bestimmt werden . Beachten Sie, dass mit der Wärmeerzeugung der Wärmefluss nicht mehr unabhängig von r ist.
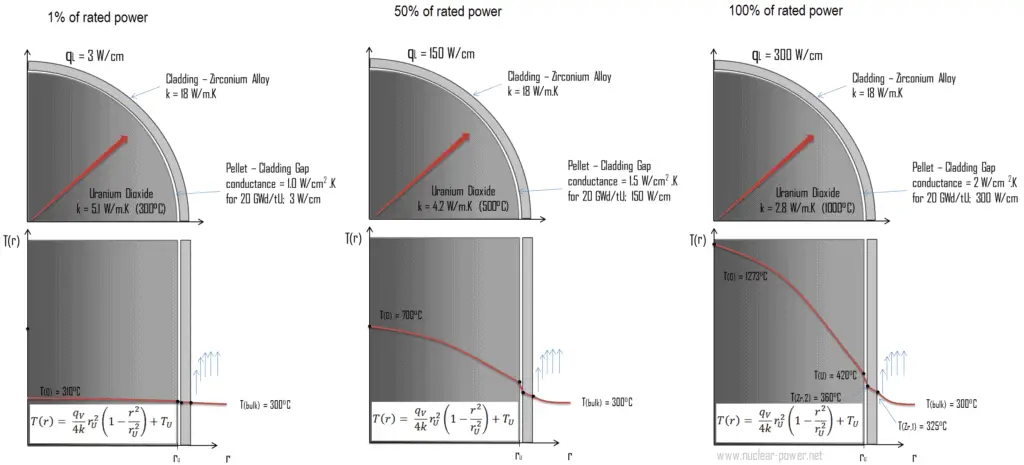
Die folgende Abbildung zeigt die Temperaturverteilung im Brennstoffpellet bei verschiedenen Leistungsstufen.
______
Die Temperatur in einem Betriebsreaktor variiert von Punkt zu Punkt innerhalb des Systems. Infolgedessen gibt es immer einen Brennstab und ein lokales Volumen , die heißer sind als alle anderen. Um diese heißen Orte zu begrenzen, müssen die Spitzenleistungsgrenzen eingeführt werden. Die Spitzenleistungsgrenzen sind mit einer Siedekrise und mit den Bedingungen verbunden, die eine Brennstoffpelletschmelze verursachen können. Metallurgische Überlegungen begrenzen jedoch die Temperatur des Brennstoffmantels und des Brennstoffpellets nach oben. Über diesen TemperaturenEs besteht die Gefahr, dass der Kraftstoff beschädigt wird. Eines der Hauptziele bei der Auslegung eines Kernreaktors besteht darin, die Wärmeabfuhr bei der gewünschten Leistung zu gewährleisten und gleichzeitig sicherzustellen, dass die maximale Brennstofftemperatur und die maximale Plattiertemperatur immer unter diesen vorgegebenen Werten liegen.
Siehe auch: Manteloberflächentemperatur
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.