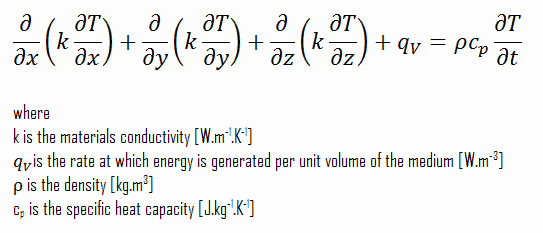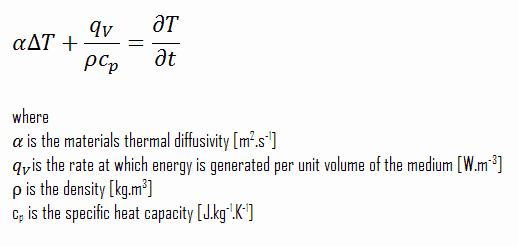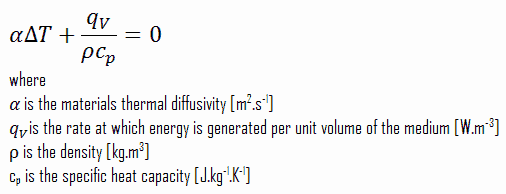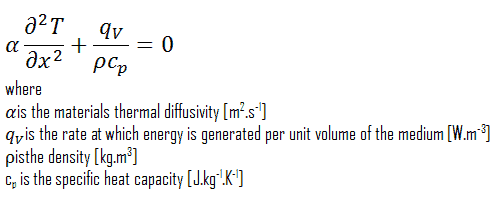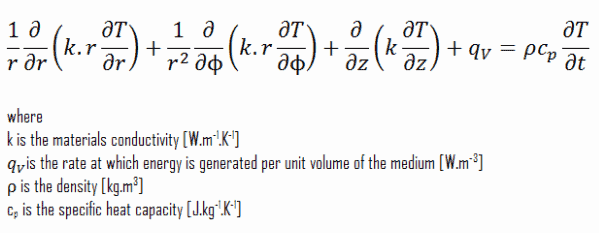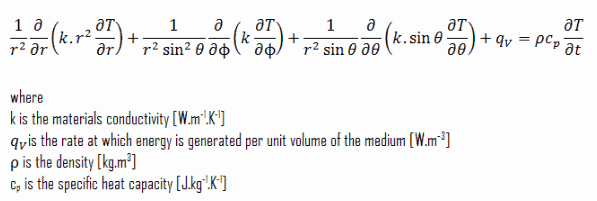O que é Equação de Calor – Equação de Condução de Calor – Definição

Equação de Calor – Equação de Condução de Calor

Nas seções anteriores, tratamos especialmente da transferência de calor unidimensional em estado estacionário, que pode ser caracterizada pela lei de Fourier de condução de calor. Mas sua aplicabilidade é muito limitada. Esta lei pressupõe transferência de calor em estado estacionário através de um corpo plano (observe que a lei de Fourier também pode ser derivada para coordenadas cilíndricas e esféricas), sem fontes de calor . É simplesmente a equação da taxa neste modo de transferência de calor, onde o gradiente de temperatura é conhecido.

Mas um grande problema na maioria das análises de condução é determinar o campo de temperatura em um meio resultante das condições impostas aos seus limites. Na engenharia, temos que resolver problemas de transferência de calor envolvendo diferentes geometrias e condições diferentes, como um elemento de combustível nuclear cilíndrico, que envolve fonte de calor interna ou a parede de uma contenção esférica. Esses problemas são mais complexos do que as análises planares que fizemos nas seções anteriores. Portanto, esses problemas serão o assunto desta seção, na qual a equação de condução de calor será introduzida e resolvida.

Equação geral de condução de calor

A equação de condução de calor é uma equação diferencial parcial que descreve a distribuição de calor (ou o campo de temperatura ) em um determinado corpo ao longo do tempo. O conhecimento detalhado do campo de temperatura é muito importante na condução térmica através de materiais. Uma vez que essa distribuição de temperatura é conhecida, o fluxo de calor de condução em qualquer ponto do material ou em sua superfície pode ser calculado pela lei de Fourier .

A equação do calor é derivada da lei de Fourier e da conservação de energia . A lei de Fourier afirma que a taxa de tempo de transferência de calor através de um material é proporcional ao gradiente negativo na temperatura e à área, perpendicularmente àquele gradiente, através do qual o calor flui.

Uma mudança na energia interna por unidade de volume no material, ΔQ, é proporcional à mudança na temperatura, Δu. Isso é:

∆Q = ρ.c _p .∆T

Forma geral

Usando essas duas equações, podemos derivar a equação geral de condução de calor:

Essa equação também é conhecida como equação de Fourier-Biot e fornece a ferramenta básica para análise de condução de calor. A partir de sua solução, podemos obter o campo de temperatura em função do tempo.

Em palavras, a equação de condução de calor afirma que:

Em qualquer ponto do meio, a taxa líquida de transferência de energia por condução em um volume unitário mais a taxa volumétrica de geração de energia térmica deve ser igual à taxa de variação da energia térmica armazenada dentro do volume.

Condutividade térmica constanteEsta equação pode ser ainda mais reduzida assumindo que a condutividade térmica seja constante e introduzindo a difusividade térmica, α = k / ρc _p :

Condutividade térmica constante e transferência de calor em estado estacionário – equação de PoissonSimplificações adicionais da forma geral da equação do calor são frequentemente possíveis. Por exemplo, em condições de estado estacionário, não pode haver alteração na quantidade de armazenamento de energia (∂T / ∂t = 0).

Equação unidimensional de calor

Uma das suposições mais poderosas é que o caso especial de transferência de calor unidimensional na direção x. Nesse caso, as derivadas em relação a ye z são eliminadas e as equações acima se reduzem a (coordenadas cartesianas):

Condução de calor em coordenadas cilíndricas e esféricas

Na engenharia, existem muitos problemas que não podem ser resolvidos em coordenadas cartesianas. Os sistemas cilíndricos e esféricos são muito comuns em engenharia térmica e, principalmente, em engenharia de energia. A equação do calor também pode ser expressa em coordenadas cilíndricas e esféricas. A equação geral de condução de calor em coordenadas cilíndricas pode ser obtida a partir de um balanço de energia em um elemento de volume em coordenadas cilíndricas e usando o operador Laplace, Δ, na forma cilíndrica e esférica .

Coordenadas cilíndricas:

Coordenadas esféricas:

A obtenção de soluções analíticas para essas equações diferenciais requer um conhecimento das técnicas de solução de equações diferenciais parciais, que estão além do escopo deste texto. Por outro lado, existem muitas simplificações e suposições que podem ser aplicadas a essas equações e que levam a resultados muito importantes. Na próxima seção, limitamos nossa consideração a casos unidimensionais de estado estacionário com condutividade térmica constante, uma vez que resultam em equações diferenciais ordinárias.

Limite e condições iniciais

Quanto a outra equação diferencial , a solução é dada por condições de contorno e iniciais . No que diz respeito às condições de contorno, existem várias possibilidades comuns que são simplesmente expressas em forma matemática.

Como a equação do calor é de segunda ordem nas coordenadas espaciais, para descrever completamente um problema de transferência de calor, duas condições de contorno devem ser dadas para cada direção do sistema de coordenadas ao longo do qual a transferência de calor é significativa. Portanto, precisamos especificar quatro condições de contorno para problemas bidimensionais e seis condições de contorno para problemas tridimensionais.

Quatro tipos de condições de contorno comumente encontradas na transferência de calor são resumidas na seção a seguir:

Condução com geração de calor

Na seção anterior, consideramos problemas de condução térmica sem fontes de calor internas . Para esses problemas, a distribuição de temperatura em um meio foi determinada apenas por condições nos limites do meio. Porém, na engenharia, muitas vezes podemos encontrar um problema, no qual as fontes internas de calor são significativas e determinam a distribuição de temperatura juntamente com as condições de contorno.

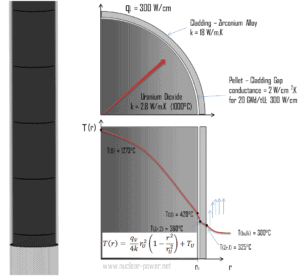
Na engenharia nuclear , esses problemas são da maior importância, uma vez que a maior parte do calor gerado no combustível nuclear é liberada dentro dos pellets de combustível e a distribuição da temperatura é determinada principalmente pela distribuição da geração de calor. Observe que, como pode ser visto na descrição dos componentes individuais da energia total liberada durante a reação de fissão, há uma quantidade significativa de energia gerada fora do combustível nuclear (barras de combustível externas). Especialmente a energia cinética dos nêutrons imediatos é amplamente gerada no refrigerante ( moderador ) . Esse fenômeno precisa ser incluído nos cálculos nucleares.

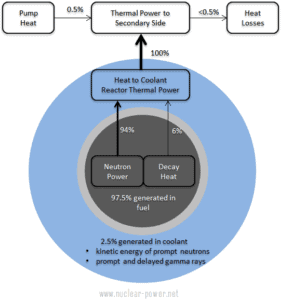
Para LWR , é geralmente aceito que cerca de 2,5% da energia total é recuperada no moderador . Essa fração de energia depende dos materiais, sua disposição dentro do reator e, portanto, do tipo de reator.

Observe que a geração de calor é um fenômeno volumétrico. Ou seja, ocorre em todo o corpo de um meio. Portanto, a taxa de geração de calor em um meio é geralmente especificada por unidade de volume e é denotada por g _V [W / m ³ ] .

A distribuição da temperatura e, consequentemente, o fluxo de calor são determinados principalmente por:

• Geometria e condições de contorno . Geometria diferente leva a um campo de temperatura completamente diferente.
• Taxa de geração de calor . A queda de temperatura no corpo aumentará com o aumento da geração de calor.
• Condutividade térmica do meio . Maior condutividade térmica levará a uma queda de temperatura mais baixa.