Trabalho em Termodinâmica
Na termodinâmica, o trabalho realizado por um sistema é a energia transferida pelo sistema para os arredores. Energia cinética, energia potencial e energia interna são formas de energia que são propriedades de um sistema. O trabalho é uma forma de energia , mas é energia em trânsito . Um sistema não contém trabalho, trabalho é um processo realizado por ou em um sistema. Em geral, o trabalho é definido para sistemas mecânicos como a ação de uma força sobre um objeto a distância.
W = F. d
Onde:
W = trabalho (J)
F = força (N)
d = deslocamento (m)
Trabalho pΔV
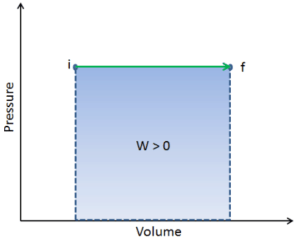
O trabalho pressão-volume (ou pΔV Work ) ocorre quando o volume V de um sistema é alterado. O trabalho pΔV é igual à área sob a curva do processo plotada no diagrama pressão-volume. É conhecido também como o trabalho de fronteira . O trabalho de limite ocorre porque a massa da substância contida no limite do sistema faz com que uma força, a pressão vezes a área da superfície, atue na superfície do limite e faça com que ela se mova. O trabalho de limite (ou pΔV Work ) ocorre quando o volume V de um sistema é alterado . É usado para calcular o trabalho de deslocamento do pistão em um sistema fechado. É o que acontece quando o vapor ou o gás contido em um dispositivo de cilindro e pistão se expande contra o pistão e força o pistão a se mover.
Exemplo:
Considere-se um pistão de atrito que é usado para proporcionar uma pressão constante de 500 kPa num cilindro contendo vapor ( vapor sobreaquecido ) de um volume de 2 m 3 a 500 K .
Calcule a temperatura final, se 3000 kJ de calor forem adicionados.
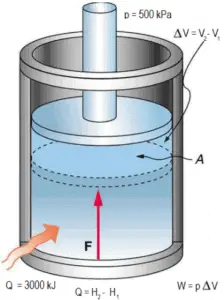
Solução:
Usando tabelas de vapor , sabemos que a entalpia específica desse vapor (500 kPa; 500 K) é de cerca de 2912 kJ / kg . Como nessa condição o vapor possui densidade de 2,2 kg / m 3 , sabemos que há cerca de 4,4 kg de vapor no pistão na entalpia de 2912 kJ / kg x 4,4 kg = 12812 kJ .
Quando usamos simplesmente Q = H 2 – H 1 , a entalpia resultante do vapor será:
H 2 = H 1 + Q = 15812 kJ
Nas tabelas de vapor , esse vapor superaquecido (15812 / 4,4 = 3593 kJ / kg) terá uma temperatura de 828 K (555 ° C) . Uma vez que nesta entalpia do vapor tem a densidade de 1,31 kg / m 3 , é óbvio que se expandiu em cerca de 2,2 / 1,31 = 1,67 (+ 67%). Portanto, o volume resultante é de 2 m 3 x 1,67 = 3,34 m 3 e ∆V = 3,34 m 3 – 2 m 3 = 1,34 m 3 .
A parte p∆V da entalpia, ou seja, o trabalho realizado é:
W = p∆V = 500 000 Pa x 1,34 m 3 = 670 kJ
———–
Durante a mudança de volume , a pressão e a temperatura também podem mudar. Para calcular esses processos, precisaríamos saber como a pressão varia com o volume do processo real pelo qual o sistema muda do estado i para o estado f . A primeira lei da termodinâmica e o trabalho podem ser expressos como:
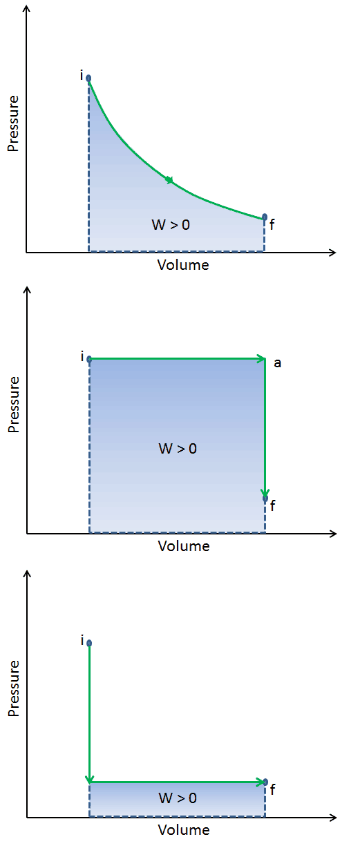
Quando um sistema termodinâmico muda de um estado inicial para um estado final , ele passa por uma série de estados intermediários . Chamamos essa série de estados de caminho . Sempre existem infinitas possibilidades para esses estados intermediários. Quando todos eles são estados de equilíbrio, o caminho pode ser plotado em um diagrama pV . Uma das conclusões mais importantes é que:
O trabalho realizado pelo sistema depende não apenas dos estados inicial e final, mas também dos estados intermediários – ou seja, no caminho.
Q e W são dependentes do caminho, enquanto ΔE int é independente do caminho. Como pode ser visto na figura (diagrama pV), o trabalho é variável dependente do caminho. A área azul representa o trabalho pΔV realizado por um sistema, que passa de um estado inicial i para um estado final f. O trabalho W é positivo porque o volume do sistema aumenta. O segundo processo mostra que o trabalho é maior e depende do caminho do processo.
Além disso, podemos conduzir o sistema através de uma série de estados formando um circuito fechado , como i ⇒ f ⇒ i . Nesse caso, o estado final é o mesmo que o estado inicial , mas o trabalho total realizado pelo sistema não é zero . Um valor positivo para o trabalho indica que o trabalho é realizado pelo sistema em seus arredores. Um valor negativo indica que o trabalho é realizado no sistema por seus arredores.
Exemplo: Trabalho Específico da Turbina
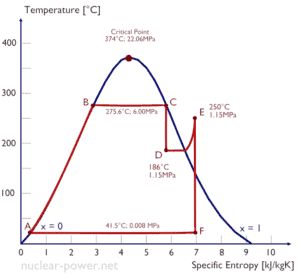
Um estágio de alta pressão da turbina a vapor opera em estado estacionário com condições de entrada de 6 MPa , t = 275,6 ° C , x = 1 (ponto C). Vapor folhas esta etapa de turbina a uma pressão de 1,15 MPa , 186 ° C e x = 0,87 (ponto D). Calcule a diferença de entalpia entre esses dois estados. Determine a transferência de trabalho específica.
A entalpia para o estado C pode ser coletada diretamente das tabelas de vapor , enquanto a entalpia para o estado D deve ser calculada usando a qualidade do vapor :
h 1, molhado = 2785 kJ / kg
h 2, molhado = h 2, s x + (1 – x) h 2, l = 2782. 0,87 + (1 – 0,87). 790 = 2420 + 103 = 2523 kJ / kg
Δh = 262 kJ / kg
Como no processo adiabático dh = dw , Δh = 262 kJ / kg é o trabalho específico da turbina .
Primeira lei em termos de entalpia dH = dQ + Vdp
A entalpia é definida como sendo a soma da energia interna E mais o produto da pressão P e volume V . Em muitas análises termodinâmicas, a soma da energia interna U e o produto da pressão pe volume V aparece; portanto, é conveniente atribuir à combinação um nome, entalpia e um símbolo distinto, H.
H = U + pV
Veja também: Entalpia
A primeira lei da termodinâmica em termos de entalpia mostra-nos por que os engenheiros usam a entalpia em ciclos termodinâmicos (por exemplo, ciclo de Brayton ou ciclo de Rankine ).
A forma clássica da lei é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira .
Como H = U + pV , portanto dH = dU + pdV + Vdp e substituímos dU = dH – pdV – Vdp na forma clássica da lei:dH – pdV – Vdp = dQ – pdV
Obtemos a lei em termos de entalpia:
dH = dQ + Vdp
ou
dH = TdS + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia . A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
É óbvio que será muito útil na análise de ambos os ciclos termodinâmicos usados na engenharia de energia, ou seja, no ciclo de Brayton e no ciclo de Rankine.
Exemplo: Primeira Lei da Termodinâmica e Ciclo de Brayton
Vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante . Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton. Esse ciclo consiste em quatro processos termodinâmicos:
-

O ciclo ideal de Brayton consiste em quatro processos termodinâmicos. Dois processos isentrópicos e dois processos isobáricos. compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Como pode ser visto, podemos descrever e calcular (por exemplo, eficiência termodinâmica) esses ciclos (da mesma forma para o ciclo de Rankine ) usando entalpias .
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
