Travailler en thermodynamique
En thermodynamique, le travail effectué par un système correspond à l’énergie transférée par le système à son environnement. L’énergie cinétique, l’énergie potentielle et l’énergie interne sont des formes d’énergie qui sont les propriétés d’un système. Le travail est une forme d’énergie , mais c’est de l’ énergie en transit . Un système ne contient pas de travail, le travail est un processus effectué par ou sur un système. En général, le travail est défini pour les systèmes mécaniques comme l’action d’une force sur un objet à distance.
W = F. ré
où:
W = travail (J)
F = force (N)
d = déplacement (m)
Travail pΔV
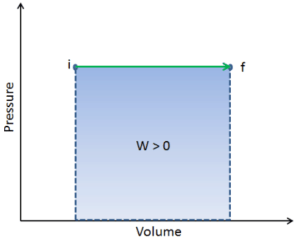
Le travail pression-volume (ou travail pΔV ) se produit lorsque le volume V d’un système change. Le travail pΔV est égal à l’aire sous la courbe de processus tracée sur le diagramme pression-volume. Il est également connu comme le travail de frontière . Le travail aux limites se produit parce que la masse de la substance contenue dans la limite du système entraîne une force, la pression multipliée par la surface, à agir sur la surface limite et à la faire bouger. Le travail aux limites (ou travail pΔV ) se produit lorsque le volume V d’un système change . Il est utilisé pour calculer le travail de déplacement de piston dans un système fermé. C’est ce qui se produit lorsque de la vapeur ou du gaz contenu dans un dispositif piston-cylindre se dilate contre le piston et force le piston à se déplacer.
Exemple:
Considérons un piston sans friction qui est utilisé pour fournir une pression constante de 500 kPa en une vapeur contenant de cylindre ( vapeur surchauffée ) d’un volume de 2 m 3 à 500 K .
Calculez la température finale, si 3000 kJ de chaleur sont ajoutés.
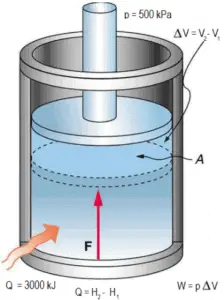
Solution:
En utilisant des tables à vapeur, nous savons que l’ enthalpie spécifique de cette vapeur (500 kPa; 500 K) est d’environ 2912 kJ / kg . Étant donné qu’à cette condition, la vapeur a une densité de 2,2 kg / m 3 , alors nous savons qu’il y a environ 4,4 kg de vapeur dans le piston à l’enthalpie de 2912 kJ / kg x 4,4 kg = 12812 kJ .
Lorsque nous utilisons simplement Q = H 2 – H 1 , l’enthalpie de vapeur résultante sera alors:
H 2 = H 1 + Q = 15812 kJ
A partir des tables à vapeur , une telle vapeur surchauffée (15812 / 4,4 = 3593 kJ / kg) aura une température de 828 K (555 ° C) . Comme à cette enthalpie, la vapeur a une densité de 1,31 kg / m 3 , il est évident qu’elle a augmenté d’environ 2,2 / 1,31 = 1,67 (+ 67%). Par conséquent, le volume résultant est de 2 m 3 x 1,67 = 3,34 m 3 et ∆V = 3,34 m 3 – 2 m 3 = 1,34 m 3 .
La partie p∆V de l’enthalpie, c’est-à-dire le travail effectué est:
W = p∆V = 500 000 Pa x 1,34 m 3 = 670 kJ
———–
Pendant le changement de volume , la pression et la température peuvent également changer. Pour calculer de tels processus, nous aurions besoin de savoir comment la pression varie avec le volume pour le processus réel par lequel le système passe de l’état i à l’état f . La première loi de la thermodynamique et du travail peut alors s’exprimer comme:
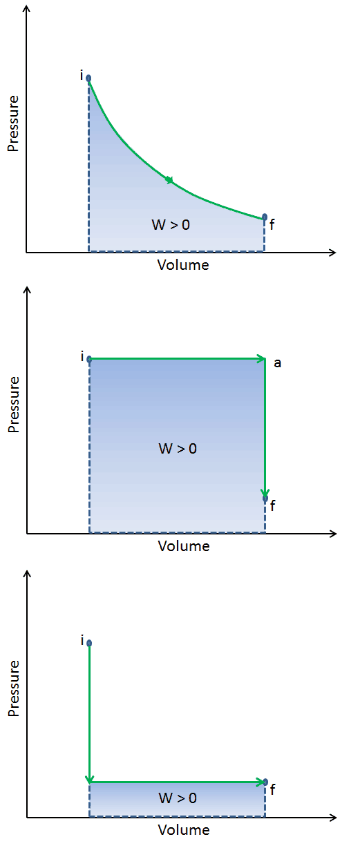
Lorsqu’un système thermodynamique passe d’un état initial à un état final , il passe par une série d’états intermédiaires . Nous appelons cette série d’états un chemin . Il existe toujours une infinité de possibilités différentes pour ces états intermédiaires. Quand ce sont tous des états d’équilibre, le chemin peut être tracé sur un diagramme pV . L’une des conclusions les plus importantes est que:
Le travail effectué par le système dépend non seulement des états initial et final, mais aussi des états intermédiaires, c’est-à-dire du chemin.
Q et W dépendent du chemin, tandis que ΔE int est indépendant du chemin. Comme le montre l’image (diagramme pV), le travail est une variable dépendante du chemin. La zone bleue représente le travail pΔV effectué par un système lorsqu’il passe d’un état initial i à un état final f. Le travail W est positif car le volume du système augmente. Le deuxième processus montre que le travail est plus important et que cela dépend du chemin du processus.
De plus, nous pouvons faire passer le système à travers une série d’états formant une boucle fermée , tels que i ⇒ f ⇒ i . Dans ce cas, l’ état final est le même que l’état initial , mais le travail total effectué par le système n’est pas nul . Une valeur positive pour le travail indique que le travail est effectué par le système sur son environnement. Une valeur négative indique que le travail est effectué sur le système par son environnement.
Exemple: travaux spécifiques aux turbines
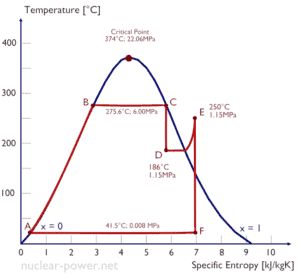
Un étage haute pression de turbine à vapeur fonctionne à l’état stable avec des conditions d’entrée de 6 MPa , t = 275,6 ° C , x = 1 (point C). La vapeur sort de cet étage de turbine à une pression de 1,15 MPa , 186 ° C et x = 0,87 (point D). Calculez la différence d’enthalpie entre ces deux états. Déterminez le transfert de travail spécifique.
L’ enthalpie pour l’état C peut être prélevée directement dans les tables de vapeur , tandis que l’enthalpie pour l’état D doit être calculée en utilisant la qualité de la vapeur :
h 1, humide = 2785 kJ / kg
h 2, humide = h 2, s x + (1 – x) h 2, l = 2782. 0,87 + (1 – 0,87). 790 = 2420 + 103 = 2523 kJ / kg
Δh = 262 kJ / kg
Puisque dans le processus adiabatique dh = dw , Δh = 262 kJ / kg est le travail spécifique de la turbine .
Première loi en termes d’enthalpie dH = dQ + Vdp
L’ enthalpie est définie comme étant la somme de l’ énergie interne E plus le produit de la pression p et de volume V . Dans de nombreuses analyses thermodynamiques, la somme de l’énergie interne U et du produit de la pression p et du volume V apparaît, il est donc commode de donner à la combinaison un nom, une enthalpie et un symbole distinct, H.
H = U + pV
Voir aussi: Enthalpie
La première loi de la thermodynamique en termes d’ enthalpie nous montre pourquoi les ingénieurs utilisent l’enthalpie dans les cycles thermodynamiques (par exemple le cycle de Brayton ou le cycle de Rankine ).
La forme classique de la loi est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites .
Nous obtenons la loi en matière d’enthalpie:
dH = dQ + Vdp
ou
dH = TdS + Vdp
Dans cette équation, le terme Vdp est un travail de processus d’écoulement. Ce travail, Vdp , est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp» , c’est-à-dire un changement de pression. Il n’y a aucun changement dans le volume de contrôle . Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Il est évident, il sera très utile dans l’analyse des deux cycles thermodynamiques utilisés en génie énergétique, c’est-à-dire dans le cycle de Brayton et le cycle de Rankine.
Exemple: Première loi de la thermodynamique et cycle de Brayton
Supposons le cycle de Brayton idéal qui décrit le fonctionnement d’un moteur thermique à pression constante . Les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérodynamique suivent également le cycle de Brayton. Ce cycle comprend quatre processus thermodynamiques:
-

Le cycle de Brayton idéal se compose de quatre processus thermodynamiques. Deux processus isentropiques et deux processus isobares. compression isentropique – l’air ambiant est aspiré dans le compresseur, où il est mis sous pression (1 → 2). Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- addition de chaleur isobare – l’air comprimé traverse ensuite une chambre de combustion, où le combustible est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- expansion isentropique – l’air chauffé sous pression se détend ensuite sur la turbine, cède son énergie. Le travail effectué par turbine est donné par W T = H 4 – H 3
- rejet de chaleur isobare – la chaleur résiduelle doit être rejetée afin de fermer le cycle. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Comme on peut le voir, nous pouvons décrire et calculer (par exemple l’efficacité thermodynamique) de tels cycles (de même pour le cycle de Rankine ) en utilisant des enthalpies .
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
