Arbeiten in Thermodynamik
In der Thermodynamik ist die von einem System geleistete Arbeit die vom System an seine Umgebung übertragene Energie. Kinetische Energie, potentielle Energie und innere Energie sind Energieformen, die Eigenschaften eines Systems sind. Arbeit ist eine Energieform , aber es ist Energie auf der Durchreise . Ein System enthält keine Arbeit, Arbeit ist ein Prozess, der von oder auf einem System ausgeführt wird. Im Allgemeinen wird Arbeit für mechanische Systeme als die Einwirkung einer Kraft auf ein Objekt über eine Distanz definiert.
W = F. d
wo:
W = Arbeit (J)
F = Kraft (N)
d = Verschiebung (m)
pΔV Arbeit
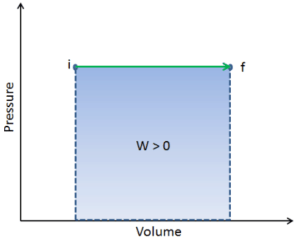
Druck-Volumen-Arbeit (oder pΔV- Arbeit ) tritt auf, wenn sich das Volumen V eines Systems ändert. Die pΔV- Arbeit ist gleich der Fläche unter der Prozesskurve, die im Druck-Volumen-Diagramm aufgetragen ist. Es ist auch als Grenzarbeit bekannt . Grenzarbeit tritt auf, weil die Masse der Substanz, die in der Systemgrenze enthalten ist, eine Kraft, den Druck mal die Oberfläche, auf die Grenzfläche einwirken lässt und sie in Bewegung versetzt. Grenzarbeit (oder pΔV- Arbeit ) tritt auf, wenn sich das Volumen V eines Systems ändert . Es wird zur Berechnung der Kolbenverdrängungsarbeit in einem geschlossenen System verwendet. Dies ist der Fall, wenn sich in einer Kolben-Zylinder-Vorrichtung enthaltener Dampf oder Gas gegen den Kolben ausdehnt und den Kolben zur Bewegung zwingt.
Beispiel:
Stellen Sie sich einen reibungslosen Kolben vor, der verwendet wird, um einen konstanten Druck von 500 kPa in einem Zylinder bereitzustellen , der Dampf ( überhitzten Dampf ) mit einem Volumen von 2 m 3 bei 500 K enthält .
Berechnen der Endtemperatur, falls 3000 kJ von Wärme hinzugefügt wird.
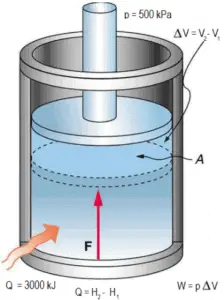
Lösung:
Anhand von Dampftabellen wissen wir, dass die spezifische Enthalpie eines solchen Dampfes (500 kPa; 500 K) etwa 2912 kJ / kg beträgt . Da der Dampf unter diesen Bedingungen eine Dichte von 2,2 kg / m 3 hat , wissen wir, dass sich bei einer Enthalpie von 2912 kJ / kg x 4,4 kg = 12812 kJ etwa 4,4 kg Dampf im Kolben befinden .
Wenn wir einfach Q = H 2 – H 1 verwenden , ist die resultierende Dampfenthalpie:
H 2 = H 1 + Q = 15812 kJ
Von Dampftabellen , wie Heißdampf (15812 / 4,4 = 3593 kJ / kg) wird eine Temperatur von haben 828 K (555 ° C) . Da der Dampf bei dieser Enthalpie eine Dichte von 1,31 kg / m 3 hat , ist es offensichtlich, dass er sich um etwa 2,2 / 1,31 = 1,67 (+ 67%) ausgedehnt hat. Daher beträgt das resultierende Volumen 2 m 3 × 1,67 = 3,34 m 3 und ∆V = 3,34 m 3 – 2 m 3 = 1,34 m 3 .
Der p∆V- Teil der Enthalpie, dh die geleistete Arbeit, ist:
W = p∆V = 500 000 Pa × 1,34 m 3 = 670 kJ
———–
Während der Volumenänderung , der Druck und Temperatur können auch geändert werden . Um solche Prozesse zu berechnen, müssten wir wissen, wie sich der Druck mit dem Volumen für den tatsächlichen Prozess ändert, durch den sich das System von Zustand i zu Zustand f ändert . Der erste Hauptsatz der Thermodynamik und der Arbeit kann dann ausgedrückt werden als:
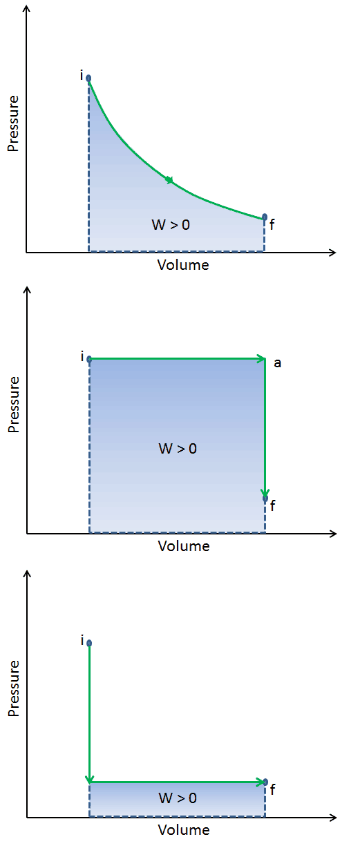
Wenn ein thermodynamisches System von einem Anfangszustand in einen Endzustand wechselt, durchläuft es eine Reihe von Zwischenzuständen . Wir nennen diese Reihe von Zuständen einen Weg . Für diese Zwischenzustände gibt es immer unendlich viele verschiedene Möglichkeiten. Wenn sie alle Gleichgewichtszustände sind, kann der Pfad in einem pV-Diagramm aufgezeichnet werden . Eine der wichtigsten Schlussfolgerungen ist:
Die vom System geleistete Arbeit hängt nicht nur von den Anfangs- und Endzuständen ab, sondern auch von den Zwischenzuständen, dh vom Pfad.
Q und W sind pfadabhängig, während ΔE int pfadunabhängig ist. Wie aus dem Bild (pV-Diagramm) ersichtlich, ist die Arbeit eine pfadabhängige Variable. Der blaue Bereich stellt die pΔV- Arbeit dar , die von einem System ausgeführt wird, wenn es von einem Anfangszustand i in einen Endzustand f übergeht. Arbeit W ist positiv, weil das Systemvolumen zunimmt. Der zweite Prozess zeigt, dass die Arbeit größer ist und vom Pfad des Prozesses abhängt.
Darüber hinaus können wir das System durch eine Reihe von Zuständen führen, die eine geschlossene Schleife bilden , wie z. B. i ⇒ f ⇒ i . In diesem Fall ist der Endzustand derselbe wie der Anfangszustand , aber die vom System geleistete Gesamtarbeit ist nicht Null . Ein positiver Wert für die Arbeit zeigt an, dass das System an seiner Umgebung arbeitet. Ein negativer Wert zeigt an, dass die Umgebung am System arbeitet.
Beispiel: Turbinenspezifische Arbeit
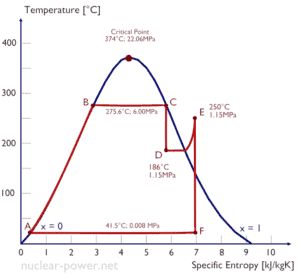
Eine Hochdruckstufe der Dampfturbine arbeitet im stationären Zustand mit Einlassbedingungen von 6 MPa , t = 275,6 ° C , x = 1 (Punkt C). Dampf verlässt diese Turbinenstufe mit einem Druck von 1,15 MPa , 186 ° C und x = 0,87 (Punkt D). Berechnen Sie die Enthalpiedifferenz zwischen diesen beiden Zuständen. Bestimmen Sie die spezifische Arbeitsübertragung.
Die Enthalpie für den Zustand C kann direkt aus Dampftabellen entnommen werden , während die Enthalpie für den Zustand D anhand der Dampfqualität berechnet werden muss :
h 1, nass = 2785 kJ / kg
h 2, nass = h 2, s x + (1 – x) h 2, l = 2782. 0,87 + (1 – 0,87). 790 = 2420 + 103 = 2523 kJ / kg
Δh = 262 kJ / kg
Da im adiabatischen Prozess dh = dw ist , ist Δh = 262 kJ / kg die turbinenspezifische Arbeit .
Erstes Gesetz in Bezug auf die Enthalpie dH = dQ + Vdp
Die Enthalpie ist definiert als die Summe aus der seinen inneren Energie E plus das Produkt des Druck p und Volumen V . In vielen thermodynamischen Analysen erscheint die Summe der inneren Energie U und des Produkts aus Druck p und Volumen V, daher ist es zweckmäßig, der Kombination einen Namen, eine Enthalpie und ein eindeutiges Symbol H zu geben.
H = U + pV
Siehe auch: Enthalpie
Der erste Hauptsatz der Thermodynamik in Bezug auf die Enthalpie zeigt uns, warum Ingenieure die Enthalpie in thermodynamischen Kreisprozessen verwenden (z. B. Brayton-Zyklus oder Rankine-Zyklus ).
Die klassische Form des Gesetzes ist die folgende Gleichung:
dU = dQ – dW
In dieser Gleichung dW gleich dW = pdV und ist bekannt als die Grenz Arbeit .
Da H = U + pV ist , ist dH = dU + pdV + Vdp und wir setzen dU = dH – pdV – Vdp in die klassische Form des Gesetzes ein:dH – pdV – Vdp = dQ – pdV
Wir erhalten das Gesetz in Bezug auf die Enthalpie:
dH = dQ + Vdp
oder
dH = TdS + Vdp
In dieser Gleichung ist der Begriff Vdp eine Flussprozessarbeit. Diese Arbeit, Vdp , wird für Open-Flow-Systeme wie eine Turbine oder eine Pumpe verwendet, bei denen ein „dp“ vorliegt , dh eine Druckänderung. Es gibt keine Änderungen in der Lautstärke . Wie zu sehen ist, vereinfacht diese Form des Gesetzes die Beschreibung der Energieübertragung . Bei konstantem Druck entspricht die Enthalpieänderung der Energie , die durch Erhitzen aus der Umgebung übertragen wird:
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der am oder vom System durchgeführten Flussprozessarbeit :
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1
Es ist offensichtlich, dass es bei der Analyse sowohl der in der Energietechnik verwendeten thermodynamischen Kreisprozessen, dh des Brayton-Zyklus als auch des Rankine-Zyklus, sehr nützlich sein wird.
Beispiel: Erster Hauptsatz der Thermodynamik und des Brayton-Zyklus
Nehmen wir den idealen Brayton-Zyklus an , der die Funktionsweise einer Wärmekraftmaschine mit konstantem Druck beschreibt . Moderne Gasturbinentriebwerke und luftatmende Strahltriebwerke folgen ebenfalls dem Brayton-Zyklus. Dieser Zyklus besteht aus vier thermodynamischen Prozessen:
-

Der ideale Brayton-Zyklus besteht aus vier thermodynamischen Prozessen. Zwei isentrope Prozesse und zwei isobare Prozesse. isentropische Kompression – Umgebungsluft wird in den Kompressor gesaugt und dort unter Druck gesetzt (1 → 2). Die für den Kompressor erforderliche Arbeit ist gegeben durch W C = H 2 – H 1 .
- isobare Wärmezufuhr – Die Druckluft strömt dann durch eine Brennkammer, in der Kraftstoff verbrannt und Luft oder ein anderes Medium erwärmt wird (2 → 3). Es ist ein Prozess mit konstantem Druck, da die Kammer zum Ein- und Ausströmen geöffnet ist. Die hinzugefügte Nettowärme ist gegeben durch Q add = H 3 – H 2
- isentropische Expansion – Die erwärmte Druckluft dehnt sich dann auf der Turbine aus und gibt ihre Energie ab. Die von der Turbine geleistete Arbeit ist gegeben durch W T = H 4 – H 3
- isobare Wärmeabgabe – Die Restwärme muss abgeführt werden, um den Kreislauf zu schließen. Die abgegebene Nettowärme ist gegeben durch Q re = H 4 – H 1
Wie zu sehen ist, können wir solche Kreisprozessen (ähnlich für den Rankine-Zyklus ) unter Verwendung von Enthalpien beschreiben und berechnen (z. B. thermodynamische Effizienz) .
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
