Facebook Instagram Youtube Twitter

What is Control Volume – Control Volume Analysis – Definition

by
A control volume is a fixed region in space chosen for the thermodynamic study of mass and energy balances for flowing systems. The boundary of the control volume may be a real or imaginary envelope. Thermal Engineering

Control Volume – Control Volume Analysis

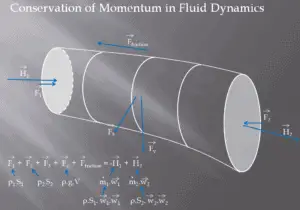Conservation of Momentum - FluidsA control volume is a fixed region in space chosen for the thermodynamic study of mass and energy balances for flowing systems. The boundary of the control volume may be a real or imaginary envelope. The control surface is the boundary of the control volume.

A control volume analysis can be used for example to determine the rate of change of momentum for a fluid. In this analysis, we will consider a streamtube (control volume) as we did for the Bernoulli equation. In this control volume any change in momentum of the fluid within a control volume is due to the action of external forces on the fluid within the volume.

See also: Momentum Formula

As can be seen from the picture the control volume method can be used to analyze the law of conservation of momentum in fluid. Control volume is an imaginary surface enclosing a volume of interest. The control volume can be fixed or moving, and it can be rigid or deformable. In order to determine all forces acting on the surfaces of the control volume we have to solve the conservation laws in this control volume.

Choosing a Control Volume

A control volume can be selected as any arbitrary volume through which fluid flows. This volume can be static, moving, and even deforming during flow. In order to solve any problem we have to solve basic conservation laws in this volume. It is very important to know all relative flow velocities to the control surface and therefore it is very important to define exactly the boundaries of the control volume during an analysis.

Example: Water Jet Striking a Stationary Plate

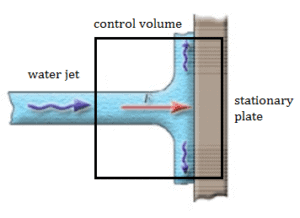Momentum Equation - Water JetA stationary plate (e.g. blade of a watermill) is used to deflect water flow at a velocity of 1 m/s and at an angle of 90°. It occurs at atmospheric pressure and the mass flow rate is equal to Q =1 m3/s.

  1. Calculate the pressure force.
  2. Calculate the body force.
  3. Calculate the total force.
  4. Calculate the resultant force.

Solution

  1. The pressure force is zero as the pressure at both the inlet and the outlets to the control volume are atmospheric.
  2. As the control volume is small we can ignore the body force due to the weight of gravity.
  3. Fx = ρ.Q.(w1x – w2x) = 1000 . 1 . (1 – 0) = 1000 N
    Fy = 0
    F = (1000, 0)
  4. The resultant force on the plane is the same magnitude but in the opposite direction as the total force F (friction and weight are neglected).

The water jet exerts on the plate the force of 1000 N in the x-direction.

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.

See also:

Fluid Dynamics

We hope, this article, Control Volume – Control Volume Analysis, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts