Facebook Instagram Youtube Twitter

What is Cyclic Process – Definition

by
A process that eventually returns a system to its initial state is called a cyclic process. Cyclic processes are often used in power engineering in heat engines. Thermal Engineering

Cyclic Process

Cyclic process - work
A process that eventually returns a system to its initial state is called a cyclic process.

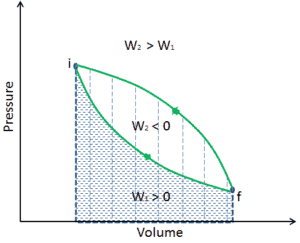
A process that eventually returns a system to its initial state is called a cyclic process. At the conclusion of a cycle, all the properties have the same value they had at the beginning. For such a process, the final state is the same as the initial state, and so the total internal energy change must be zero. Steam (water) that circulates through a closed cooling loop undergoes a cycle. The first law of thermodynamics is then:

dEint = 0, dQ = dW

Thus, the net work done during the process must exactly equal the net amount of energy transferred as heat. It must be noted, according to the second law of thermodynamics, not all heat provided to a cycle can be transformed into an equal amount of work, some heat rejection must take place.

Example of Cyclic Process – Brayton Cycle

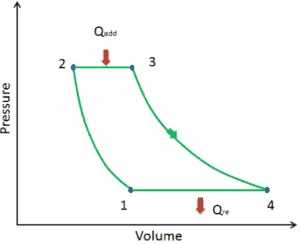
first law - example - brayton cycle
Ideal Brayton cycle consist of four thermodynamic processes. Two isentropic processes and two isobaric processes.

Let assume the ideal Brayton cycle that describes the workings of a constant pressure heat engine. Modern gas turbine engines and airbreathing jet engines also follow the Brayton cycle. This cycle consist of four thermodynamic processes:

Ideal Brayton cycle consist of four thermodynamic processes. Two isentropic processes and two isobaric processes.

  1. isentropic compression – ambient air is drawn into the compressor, where it is pressurized (1 → 2). The work required for the compressor is given by WC = H2 – H1.
  2. isobaric heat addition – the compressed air then runs through a combustion chamber, where fuel is burned and air or another medium is heated (2 → 3). It is a constant-pressure process, since the chamber is open to flow in and out. The net heat added is given by Qadd = H3 – H2
  3. isentropic expansion – the heated, pressurized air then expands on turbine, gives up its energy. The work done by turbine is given by WT = H4 – H3
  4. isobaric heat rejection – the residual heat must be rejected in order to close the cycle. The net heat rejected is given by Qre = H4 – H1

As can be seen, we can describe and calculate (e.g. thermal efficiency) such cycles (similarly for Rankine cycle) using enthalpies.

See also: Thermal Efficiency of Brayton Cycle

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

Another References:

  1. Car Recycling

See also:

Thermodynamic Processes

We hope, this article, Cyclic Process, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts