Proceso cíclico
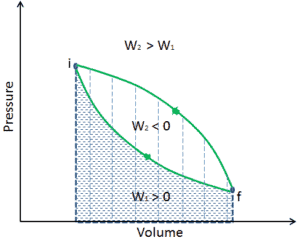
Un proceso que finalmente devuelve un sistema a su estado inicial se denomina proceso cíclico . Al final de un ciclo, todas las propiedades tienen el mismo valor que tenían al principio. Para tal proceso, el estado final es el mismo que el estado inicial , por lo que el cambio total de energía interna debe ser cero. El vapor (agua) que circula a través de un circuito cerrado de enfriamiento experimenta un ciclo. La primera ley de la termodinámica es entonces:
dE int = 0, dQ = dW
Por lo tanto, el trabajo neto realizado durante el proceso debe ser exactamente igual a la cantidad neta de energía transferida como calor. Debe tenerse en cuenta que, de acuerdo con la segunda ley de la termodinámica , no todo el calor proporcionado a un ciclo puede transformarse en una cantidad igual de trabajo, debe producirse un cierto rechazo de calor .
Ejemplo de proceso cíclico: ciclo de Brayton

Supongamos el ciclo Brayton ideal que describe el funcionamiento de un motor de calor a presión constante . Los modernos motores de turbina de gas y los motores de inyección de aire también siguen el ciclo de Brayton. Este ciclo consta de cuatro procesos termodinámicos:
El ciclo ideal de Brayton consiste en cuatro procesos termodinámicos. Dos procesos isentrópicos y dos procesos isobáricos.
- Compresión isentrópica : el aire ambiente ingresa al compresor, donde se presuriza (1 → 2). El trabajo requerido para el compresor viene dado por W C = H 2 – H 1 .
- adición de calor isobárico : el aire comprimido pasa a través de una cámara de combustión, donde se quema el combustible y se calienta el aire u otro medio (2 → 3). Es un proceso de presión constante, ya que la cámara está abierta para fluir hacia adentro y hacia afuera. El calor neto agregado viene dado por Q add = H 3 – H 2
- Expansión isentrópica : el aire calentado y presurizado se expande en la turbina y entrega su energía. El trabajo realizado por la turbina viene dado por W T = H 4 – H 3
- rechazo de calor isobárico : el calor residual debe rechazarse para cerrar el ciclo. El calor neto rechazado viene dado por Q re = H 4 – H 1
Como se puede ver, podemos describir y calcular (por ejemplo, eficiencia térmica ) tales ciclos (de manera similar para el ciclo de Rankine ) usando entalpías .
Ver también: Eficiencia térmica del ciclo de Brayton
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.