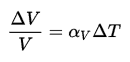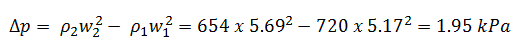What is Density

Density is defined as the mass per unit volume. It is an intensive property, which is mathematically defined as mass divided by volume:
ρ = m/V
In words, the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance. The standard SI unit is kilograms per cubic meter (kg/m3). The Standard English unit is pounds mass per cubic foot (lbm/ft3). The density (ρ) of a substance is the reciprocal of its specific volume (ν).
ρ = m/V = 1/ρ
Specific volume is an intensive variable, whereas volume is an extensive variable. The standard unit for specific volume in the SI system is cubic meters per kilogram (m3/kg). The standard unit in the English system is cubic feet per pound mass (ft3/lbm).
Densest Materials on the Earth
Since nucleons (protons and neutrons) make up most of the mass of ordinary atoms, the density of normal matter tends to be limited by how closely we can pack these nucleons and depends on the internal atomic structure of a substance. The densest material found on earth is the metal osmium, but its density pales by comparison to the densities of exotic astronomical objects such as white dwarf stars and neutron stars.
List of densest materials:
- Osmium – 22.6 x 103 kg/m3
- Iridium – 22.4 x 103 kg/m3
- Platinum – 21.5 x 103 kg/m3
- Rhenium – 21.0 x 103 kg/m3
- Plutonium – 19.8 x 103 kg/m3
- Gold – 19.3 x 103 kg/m3
- Tungsten – 19.3 x 103 kg/m3
- Uranium – 18.8 x 103 kg/m3
- Tantalum – 16.6 x 103 kg/m3
- Mercury – 13.6 x 103 kg/m3
- Rhodium – 12.4 x 103 kg/m3
- Thorium – 11.7 x 103 kg/m3
- Lead – 11.3 x 103 kg/m3
- Silver – 10.5 x 103 kg/m3
It must be noted, plutonium is a man-made isotope and is created from uranium in nuclear reactors. But, In fact, scientists have found trace amounts of naturally-occurring plutonium.
If we include man made elements, the densest so far is Hassium. Hassium is a chemical element with symbol Hs and atomic number 108. It is a synthetic element (first synthesised at Hasse in Germany) and radioactive. The most stable known isotope, 269Hs, has a half-life of approximately 9.7 seconds. It has an estimated density of 40.7 x 103 kg/m3. The density of Hassium results from its high atomic weight and from the significant decrease in ionic radii of the elements in the lanthanide series, known as lanthanide and actinide contraction.
The density of Hassium is followed by Meitnerium (element 109, named after the physicist Lise Meitner), which has an estimated density of 37.4 x 103 kg/m3.
Density of various Materials – Examples
Density of Nuclear Matter
Nuclear density is the density of the nucleus of an atom. It is the ratio of mass per unit volume inside the nucleus. Since atomic nucleus carries most of atom’s mass and atomic nucleus is very small in comparison to entire atom, the nuclear density is very high.
The nuclear density for a typical nucleus can be approximately calculated from the size of the nucleus and from its mass. Typical nuclear radii are of the order 10−14 m. Assuming spherical shape, nuclear radii can be calculated according to following formula:
r = r0 . A1/3
where r0 = 1.2 x 10-15 m = 1.2 fm
For example, natural uranium consists primarily of isotope 238U (99.28%), therefore the atomic mass of uranium element is close to the atomic mass of 238U isotope (238.03u). Its radius of this nucleus will be:
r = r0 . A1/3 = 7.44 fm.
Assuming it is spherical, its volume will be:
V = 4πr3/3 = 1.73 x 10-42 m3.
The usual definition of nuclear density gives for its density:
ρnucleus = m / V = 238 x 1.66 x 10-27 / (1.73 x 10-42) = 2.3 x 1017 kg/m3.
Thus, the density of nuclear material is more than 2.1014 times greater than that of water. It is an immense density. The descriptive term nuclear density is also applied to situations where similarly high densities occur, such as within neutron stars. Such immense densities are also found in neutron stars.
We hope, this article, Density – Physics, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.