Facebook Instagram Youtube Twitter

What is Example: Isentropic Turbine Efficiency – Definition

by
Calculate the work done by this turbine and calculate the real temperature at the exit of the turbine, when the isentropic turbine efficiency is ηT = 0.91 (91%). Thermal Engineering

Example: Isentropic Turbine Efficiency

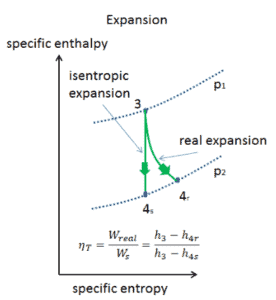
Isentropic vs. adiabatic expansion
Isentropic process is a special case of adiabatic processes. It is a reversible adiabatic process. An isentropic process can also be called a constant entropy process.

Assume an isentropic expansion of helium (3 → 4) in a gas turbine. In this turbines the high-pressure stage receives gas (point 3 at the figure; p3 = 6.7 MPa; T3 = 1190 K (917°C)) from a heat exchanger and exhaust it to another heat exchanger, where the outlet pressure is p4 = 2.78 MPa (point 4). The temperature (for isentropic process) of the gas at the exit of the turbine is T4s = 839 K (566°C).

Calculate the work done by this turbine and calculate the real temperature at the exit of the turbine, when the isentropic turbine efficiency is ηT = 0.91 (91%).

Solution:

From the first law of thermodynamics, the work done by turbine in an isentropic process can be calculated from:

WT = h3 – h4s     →     WTs = cp (T3 – T4s)

From Ideal Gas Law we know, that the molar specific heat of a monatomic ideal gas is:

Cv = 3/2R = 12.5 J/mol K and Cp = Cv + R = 5/2R = 20.8 J/mol K

We transfer the specific heat capacities into units of J/kg K via:

cp = Cp . 1/M (molar weight of helium) = 20.8 x 4.10-3 = 5200 J/kg K

The work done by gas turbine in isentropic process is then:

WT,s = cp (T3 – T4s) = 5200 x (1190 – 839) = 1.825 MJ/kg

The real work done by gas turbine in adiabatic process is then:
WT,real = cp (T3 – T4s) . ηT = 5200 x (1190 – 839) x 0.91 = 1.661 MJ/kg

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Isentropic Process

We hope, this article, Example: Isentropic Turbine Efficiency, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts