Enthalpy in Extensive Units
H = U + pV
Enthalpy is an extensive quantity, it depends on the size of the system, or on the amount of substance it contains. The SI unit of enthalpy is the joule (J). It is the energy contained within the system, excluding the kinetic energy of motion of the system as a whole and the potential energy of the system as a whole due to external force fields. It is the thermodynamic quantity equivalent to the total heat content of a system.
On the other hand, energy can be stored in the chemical bonds between the atoms that make up the molecules. This energy storage on the atomic level includes energy associated with electron orbital states, nuclear spin, and binding forces in the nucleus.
Enthalpy is represented by the symbol H, and the change in enthalpy in a process is H2 – H1.
There are expressions in terms of more familiar variables such as temperature and pressure:
dH = CpdT + V(1-αT)dp
Where Cp is the heat capacity at constant pressure and α is the coefficient of (cubic) thermal expansion. For ideal gas αT = 1 and therefore:
dH = CpdT
Example: Frictionless Piston – Heat – Enthalpy
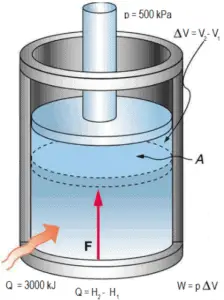
A frictionless piston is used to provide a constant pressure of 500 kPa in a cylinder containing steam (superheated steam) of a volume of 2 m3 at 500 K. Calculate the final temperature, if 3000 kJ of heat is added.
Solution:
Using steam tables we know, that the specific enthalpy of such steam (500 kPa; 500 K) is about 2912 kJ/kg. Since at this condition the steam has density of 2.2 kg/m3, then we know there is about 4.4 kg of steam in the piston at enthalpy of 2912 kJ/kg x 4.4 kg = 12812 kJ.
When we use simply Q = H2 − H1, then the resulting enthalpy of steam will be:
H2 = H1 + Q = 15812 kJ
From steam tables, such superheated steam (15812/4.4 = 3593 kJ/kg) will have a temperature of 828 K (555°C). Since at this enthalpy the steam have density of 1.31 kg/m3, it is obvious that it has expanded by about 2.2/1.31 = 1.67 (+67%). Therefore the resulting volume is 2 m3 x 1.67 = 3.34 m3 and ∆V = 3.34 m3 – 2 m3 = 1.34 m3.
The p∆V part of enthalpy, i.e. the work done is:
W = p∆V = 500 000 Pa x 1.34 m3 = 670 kJ
Example: Energy Balance in a Steam Generator
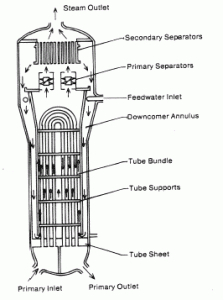
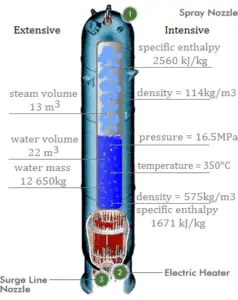
Calculate the amount of primary coolant, which is required to evaporate 1 kg of feedwater in a typical steam generator. Assume that there are no energy losses, this is only idealized example.
Balance of the primary circuit
The hot primary coolant (water 330°C; 626°F; 16MPa) is pumped into the steam generator through primary inlet. The primary coolant leaves (water 295°C; 563°F; 16MPa) the steam generator through primary outlet.
hI, inlet = 1516 kJ/kg
=> ΔhI = -206 kJ/kg
hI, outlet = 1310 kJ/kg
Balance of the feedwater
The feedwater (water 230°C; 446°F; 6,5MPa) is pumped into the steam generator through the feedwater inlet. The feedwater (secondary circuit) is heated from ~230°C 446°F to the boiling point of that fluid (280°C; 536°F; 6,5MPa). Feedwater is then evaporated and the pressurized steam (saturated steam 280°C; 536°F; 6,5 MPa) leaves the steam generator through steam outlet and continues to the steam turbine.
hII, inlet = 991 kJ/kg
=> ΔhII = 1789 kJ/kg
hII, outlet = 2780 kJ/kg
Balance of the steam generator
Since the difference in specific enthalpies is less for primary coolant than for feedwater, it is obvious that the amount of primary coolant will be higher than 1kg. To produce of 1 kg of saturated steam from feedwater, about 1789/206 x 1 kg = 8.68 kg of primary coolant is required.
Example: Combustion of Hydrogen
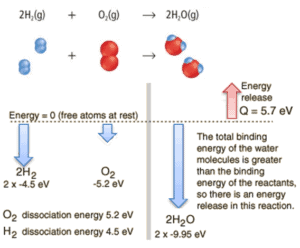
Consider the combustion of hydrogen in air. In a flame of pure hydrogen gas, burning in air, the hydrogen (H2) reacts with oxygen (O2) to form water (H2O) and releases energy.
Energetically, the process can be considered to require the energy to dissociate the H2 and O2, but then the bonding of the H2O returns the system to a bound state with negative potential. It is actually more negative than the bound states of the reactants, and the formation of the two water molecules is therefore an exothermic reaction, which releases 5.7 eV of energy. In words of enthalpy, the enthalpy of combustion is −286 kJ/mol:
2H2(g) + O2(g) → 2H2O(g)
In words of enthalpy, the enthalpy of combustion is −286 kJ/mol (energy per mol of molecular hydrogen):
2H2(g) + O2(g) → 2H2O(l) +572 kJ
The balance of energy before and after the reaction can be illustrated schematically with the state in which all atoms are free taken as the reference for energy.
Example: Enthalpy of Wet Steam
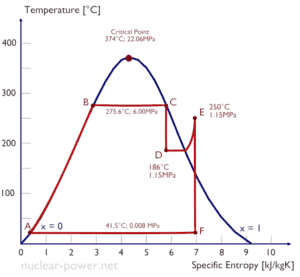
A high-pressure stage of steam turbine operates at steady state with inlet conditions of 6 MPa, t = 275.6°C, x = 1 (point C). Steam leaves this stage of turbine at a pressure of 1.15 MPa, 186°C and x = 0.87 (point D). Calculate the enthalpy difference between these two states.
The enthalpy for the state C can be picked directly from steam tables, whereas the enthalpy for the state D must be calculated using vapor quality:
h1, wet = 2785 kJ/kg
h2, wet = h2,s x + (1 – x ) h2,l = 2782 . 0.87 + (1 – 0.87) . 790 = 2420 + 103 = 2523 kJ/kg
Δh = 262 kJ/kg
We hope, this article, Example of Enthalpy – Calculation, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.