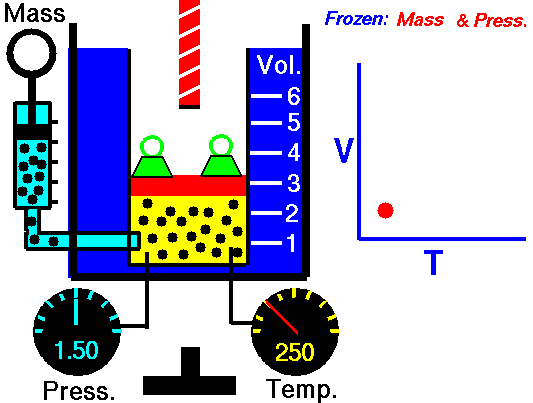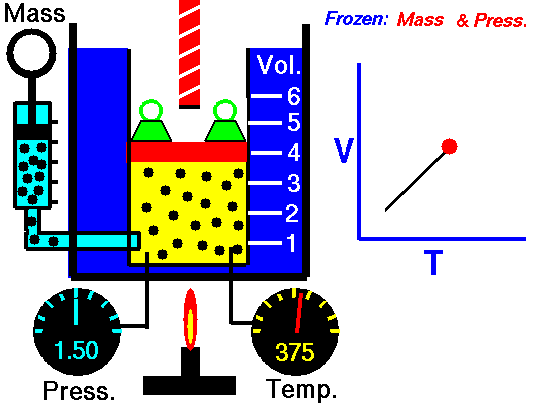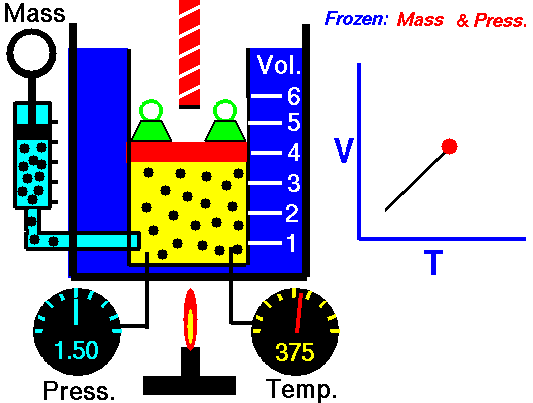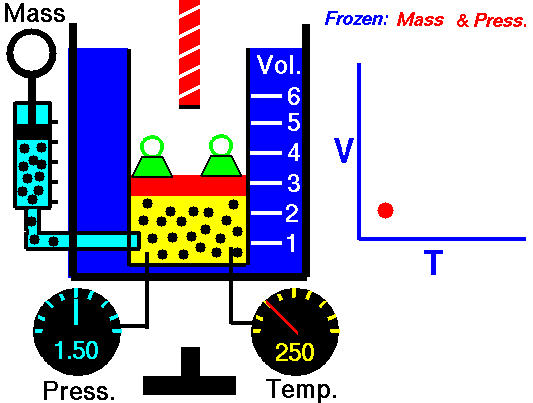
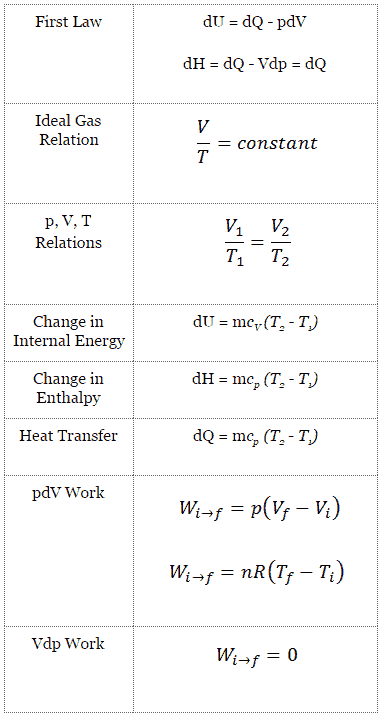Facebook Instagram Youtube Twitter

What is Isobaric Process – Heat and Energy – Definition

by
Isobaric Process – Heat and Energy. In an isobaric process and the ideal gas, part of heat added to the system will be used to do work and part of heat added will increase the internal energy. Thermal Engineering

Isobaric Process – Heat and Energy

Isobaric Process – Heat and Energy

The classical form of the first law of thermodynamics is the following equation:

dU = dQ – dW

In this equation dW is equal to dW = pdV and is known as the boundary work.

In an isobaric process and the ideal gas, part of heat added to the system will be used to do work and part of heat added will increase the internal energy (increase the temperature).  Therefore it is convenient to use the enthalpy instead of the internal energy.Since H = U + pV, therefore dH = dU + pdV + Vdp and we substitute dU = dH – pdV – Vdp into the classical form of the law:

dH – pdV – Vdp = dQ – pdV

We obtain the law in terms of enthalpy:

dH = dQ + Vdp

or

dH = TdS + Vdp

In this equation the term Vdp is a flow process work. This work,  Vdp, is used for open flow systems like a turbine or a pump in which there is a “dp”, i.e. change in pressure. There are no changes in control volume. As can be seen, this form of the law simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating:

Isobaric process (Vdp = 0):

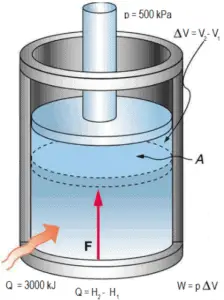
dH = dQ     →     Q = H2 – H1

At constant entropy, i.e. in isentropic process, the enthalpy change equals the flow process work done on or by the system.

Isentropic process (dQ = 0):

dH = Vdp     →     W = H2 – H1

It is obvious, it will be very useful in analysis of both thermodynamic cycles used in power engineering, i.e. in Brayton cycle and Rankine cycle.

Isobaric process - main characteristics
Isobaric process – main characteristics
Charles's Law is one of the gas laws.
For a fixed mass of gas at constant pressure, the volume is directly proportional to the Kelvin temperature. Source: grc.nasa.gov NASA copyright policy states that “NASA material is not protected by copyright unless noted”.
 
Example: Frictionless Piston – Heat – Enthalpy
Enthalpy - Example - A frictionless piston
Calculate the final temperature, if 3000 kJ of heat is added.

A frictionless piston is used to provide a constant pressure of 500 kPa in a cylinder containing steam (superheated steam) of a volume of 2 m3  at 500 K. Calculate the final temperature, if 3000 kJ of heat is added.

Solution:

Using steam tables we know, that the specific enthalpy of such steam (500 kPa; 500 K) is about 2912 kJ/kg. Since at this condition the steam has density of 2.2 kg/m3, then we know there is about 4.4 kg of steam in the piston at enthalpy of 2912 kJ/kg x 4.4 kg = 12812 kJ.

When we use simply Q = H2 − H1, then the resulting enthalpy of steam will be:

H2 = H1 + Q = 15812 kJ

From steam tables, such superheated steam (15812/4.4 = 3593 kJ/kg) will have a temperature of 828 K (555°C). Since at this enthalpy the steam have density of 1.31 kg/m3, it is obvious that it has expanded by about 2.2/1.31 = 1.67 (+67%). Therefore the resulting volume is 2 m3 x 1.67 = 3.34 m3 and ∆V = 3.34 m3 – 2 m3 = 1.34 m3.

The p∆V part of enthalpy, i.e. the work done is:

W = p∆V = 500 000 Pa x 1.34 m3 = 670 kJ

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Isobaric Process

We hope, this article, Isobaric Process – Heat and Energy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts