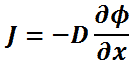Facebook Instagram Youtube Twitter

What is Sherwood Number – Definition

by
The Sherwood number is a dimensionless number, named after Thomas Kilgore Sherwood. The Sherwood number is defined as the ratio of the convective mass transfer to the mass diffusivity. Thermal Engineering

What is Sherwood Number

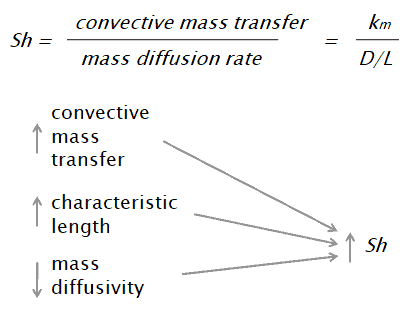
The Sherwood number is a dimensionless number, named after Thomas Kilgore Sherwood. The Sherwood number is defined as the ratio of the convective mass transfer to the mass diffusivity.

The Nusselt and Sherwood numbers represent the effectiveness of heat and mass convection at the surface. The Sherwood number is to the concentration boundary layer what the Nusselt number is to the thermal boundary layer.

The Sherwood number is defined as:

sherwood number - definition - formula

where:

km is convective mass transfer coefficient [m/s]

L is a characteristic length [m]

D is the mass diffusivity [m2/s]

For example, the Sherwood number for a single sphere can be expressed as:

Sh = Sh0 + C.RemSc1/3

where Sh0 is the Sherwood number due only to natural convection and not forced convection.

Diffusivity is encountered in Fick’s law, which states:

If the concentration of a solute in one region is greater than in another of a solution, the solute diffuses from the region of higher concentration to the region of lower concentration, with a magnitude that is proportional to the concentration gradient.

In one (spatial) dimension, the law is:

Ficks Law - equation

where:

  • J is the diffusion flux,
  • D is the diffusion coefficient,
  • φ (for ideal mixtures) is the concentration.

The use of this law in nuclear reactor theory leads to the diffusion approximation.

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Introduction to Heat Transfer

We hope, this article, Sherwood Number, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts