Facebook Instagram Youtube Twitter

What is Solution of Navier-Stokes Equation – Definition

by
Even though the Navier-Stokes equations have only a limited number of known analytical solutions, they are amenable to fine-gridded computer modeling. Solution of Navier-Stokes Equations

Solution of Navier-Stokes Equations

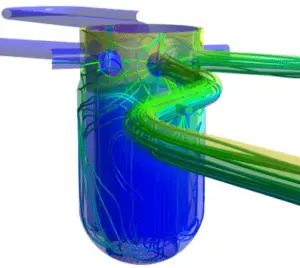
Fluid Dynamics
CFD numerical simulation
Source: CFD development group – hzdr.de

Even though the Navier-Stokes equations have only a limited number of known analytical solutions, they are amenable to fine-gridded computer modeling. The main tool available for their analysis is CFD analysis. CFD is a branch of fluid mechanics that uses numerical analysis and algorithms to solve and analyze problems that involve turbulent fluid flows. It is widely accepted that the Navier–Stokes equations (or simplified Reynolds-averaged Navier–Stokes equations) are capable of exhibiting turbulent solutions, and these equations are the basis for essentially all CFD codes. It is possible now to achieve approximate, but realistic, CFD results for a wide variety of complex two- and three-dimensional viscous flows.

The Navier–Stokes equations are also of great interest in a purely mathematical sense. Unfortunately, the highly intermittent and irregular character of turbulent flow complicates all analyses. It has not yet been proven that in three dimensions solutions always exist, or that if they do exist, then they are smooth. In fact, general solution of the Navier-Stokes equations with turbulences is often said to be the “last unsolved problem in classical mathemetical physics.”

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
  10. White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

See also:

Navier-Stokes Equations

We hope, this article, Solution of Navier-Stokes Equation, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts