Facebook Instagram Youtube Twitter

What is Spinning ball in an airflow – Bernoulli’s Effect – Definition

by
Suppose a ball is spinning as it travels through the air. As the ball spins, the surface friction of the ball with the surrounding air drags a thin layer of air with it. Thermal Engineering

Bernoulli’s Equation

Bernoulli Equation; PrincipleThe Bernoulli’s equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in following points:

  • steady flow system,
  • density is constant (which also means the fluid is incompressible),
  • no work is done on or by the fluid,
  • no heat is transferred to or from the fluid,
  • no change occurs in the internal energy,
  • the equation relates the states at two points along a single streamline (not conditions on two different streamlines)

Under these conditions, the general energy equation is simplified to:

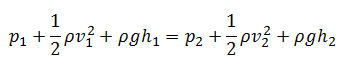
Bernoulli Theorem - Equation
This equation is the most famous equation in fluid dynamics. The Bernoulli’s equation describes the qualitative behavior flowing fluid that is usually labeled with the term Bernoulli’s effect. This effect causes the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive, but seems less so when you consider pressure to be energy density. In the high velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy. The dimensions of terms in the equation are kinetic energy per unit volume.

Bernoulli’s Effect – Spinning ball in an airflow

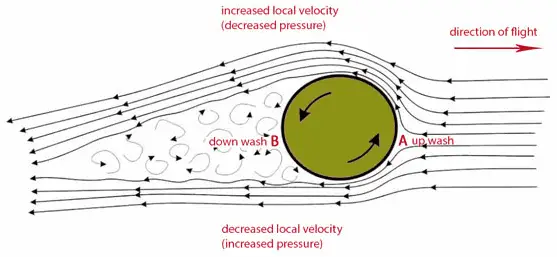
Bernoulli Principle - Spinning ballThe Bernoulli’s effect has another interesting interesting consequence. Suppose a ball is spinning as it travels through the air. As the ball spins, the surface friction of the ball with the surrounding air drags a thin layer (referred to as the boundary layer) of air with it. It can be seen from the picture the boundary layer is on one side traveling in the same direction as the air stream that is flowing around the ball (the upper arrow) and on the other side, the boundary layer is traveling in the opposite direction (the bottom arrow). On the side of the ball where the air stream and boundary layer are moving in the opposite direction (the bottom arrow) to each other friction between the two slows the air stream. On the opposite side these layers are moving in the same direction and the stream moves faster.

According to Bernoulli’s principle, faster moving air exerts less pressure, and therefore the air must exert an upward force on the ball. In fact, in this case the use of Bernoulli’s principle may not be correct. The Bernoulli’s principle assumes incompressibility of the air, but in reality the air is easily compressible. But there are more limitations of explanations based on Bernoulli’s principle.

The work of Robert G. Watts and Ricardo Ferrer (The lateral forces on a spinning sphere: Aerodynamics of a curveball) this effect can be explained by another model which gives important attention to the spinning boundary layer of air around the ball. On the side of the ball where the air stream and boundary layer are moving in the opposite direction (the bottom arrow), the boundary layer tends to separate prematurely. On the side of the ball where the air stream and boundary layer are moving in the same direction , the boundary layer carries further around the ball before it separates into turbulent flow. This gives a flow deflection of the airstream in one direction behind the ball. The rotating ball generates lift by exerting a downward force on the air as it flows past. According to Newton’s third law, the air must exert an upward force on the ball.

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.

See also:

Bernoulli’s Principle

We hope, this article, Spinning ball in an airflow – Bernoulli’s Effect, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts