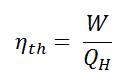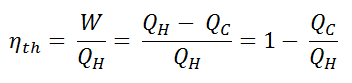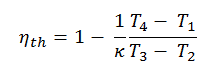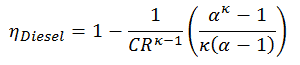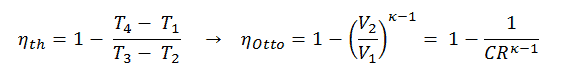Facebook Instagram Youtube Twitter

What is Thermal Efficiency for Diesel Cycle – Definition

by
In general, engines using the Diesel cycle are usually more efficient, than engines using the Otto cycle. The diesel engine has the highest thermal efficiency of any practical combustion engine. Thermal Engineering

Thermal Efficiency for Diesel Cycle

Since Carnot’s principle states that no engine can be more efficient than a reversible engine (a Carnot heat engine) operating between the same high temperature and low temperature reservoirs, the Diesel engine must have lower efficiency than the Carnot efficiency. A typical diesel automotive engine operates at around 30% to 35% of thermal efficiency. About 65-70% is rejected as waste heat without being converted into useful work, i.e. work delivered to wheels. In general, engines using the Diesel cycle are usually more efficient, than engines using the Otto cycle. The diesel engine has the highest thermal efficiency of any practical combustion engine. Low-speed diesel engines (as used in ships) can have a thermal efficiency that exceeds 50%. The largest diesel engine in the world peaks at 51.7%.

In general the thermal efficiency, ηth, of any heat engine is defined as the ratio of the work it does, W, to the heat input at the high temperature, QH.

thermal efficiency formula - 1

The thermal efficiency, ηth, represents the fraction of heat, QH, that is converted to work. Since energy is conserved according to the first law of thermodynamics and energy cannot be be converted to work completely, the heat input, QH, must equal the work done, W, plus the heat that must be dissipated as waste heat QC into the environment. Therefore we can rewrite the formula for thermal efficiency as:

thermal efficiency formula - 2

The heat absorbed occurs during combustion of fuel-air mixture, when the spark occurs, roughly at constant volume. Since during an isochoric process there is no work done by or on the system, the first law of thermodynamics dictates ∆U = ∆Q. Therefore the heat added and rejected are given by:

Qadd = mcp (T3 – T2)

Qout = mcv (T4 – T1)

Substituting these expressions for the heat added and rejected in the expression for thermal efficiency yields:

This equation can be rearranged to the form with the compression ratio and the cut-off ratio. Thermal efficiency for Diesel cycle:

where

  • ηDiesel is the maximum thermal efficiency of a Diesel cycle
  • α is the cut-off ration V3/V2 (i.e. the ratio of volumes at the end and start of the combustion phase)
  • CR is the compression ratio
  • κ = cp/cv = 1.4

It is very useful conclusion, because it is desirable to achieve a high compression ratio to extract more mechanical energy from a given mass of the fuel. As we have concluded in previous section the air-standard Otto cycle thermal efficiency is also a function of compression ratio and κ.

thermal efficiency - Otto Cycle - Compression ratio

When we compare these to formulae, it can be seen that for a given compression ratio (CR), the Otto cycle will be more efficient than the Diesel cycle . But diesel engines are usually be more efficient since they are able to operate at higher compression ratios.

In ordinary Otto engines the compression ratio has its limits. The compression ratio in a gasoline-powered engine will usually not be much higher than 10:1. Higher compression ratios will make gasoline engines subject to engine knocking, caused by autoignition an unburned mixture, if lower octane-rated fuel is used. In diesel engines there is minimal risk of autoignition of the fuel, because diesel engines are compression-ignition engines and there is no fuel in the cylinder at the beginning of the compression stroke.

See also: Diesel Cycle – Problem with Solution

See also: Compression Ratio

 
Efficiency of Engines in Transportation
  • In the middle of twentieth century, a typical steam locomotive had a thermal efficiency of about 6%. That means for every 100 MJ of coal burned, 6 MJ of mechanical power were produced.
  • A typical gasoline automotive engine operates at around 25% to 30% of thermal efficiency. About 70-75% is rejected as waste heat without being converted into useful work, i.e. work delivered to wheels.
  • A typical diesel automotive engine operates at around 30% to 35%. In general, engines using the Diesel cycle are usually more efficient.
  • In 2014, new regulations were introduced for Formula 1 cars. These motorsport regulations have pushed teams to develop highly efficient power units. According to Mercedes, their power unit is now achieving more than 45% and close to 50% thermal efficiency, i.e. 45 – 50% of the potential energy in the fuel is delivered to wheels.
  • The diesel engine has the highest thermal efficiency of any practical combustion engine. Low-speed diesel engines (as used in ships) can have a thermal efficiency that exceeds 50%. The largest diesel engine in the world peaks at 51.7%.
 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

Other References:

Diesel Engine – Car Recycling

See also:

Diesel Cycle

We hope, this article, Thermal Efficiency for Diesel Cycle, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts