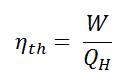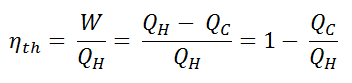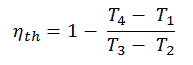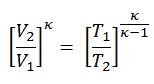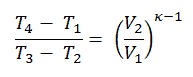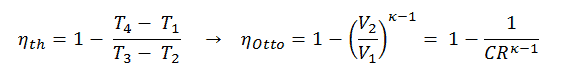Facebook Instagram Youtube Twitter

What is Thermal Efficiency for Otto Cycle – Definition

by
The air-standard Otto cycle thermal efficiency is a function of compression ratio and κ. A typical gasoline automotive engine operates at around 25% to 30% of thermal efficiency. Thermal Engineering

Thermal Efficiency for Otto Cycle

In general the thermal efficiency, ηth, of any heat engine is defined as the ratio of the work it does, W, to the heat input at the high temperature, QH.

thermal efficiency formula - 1

The thermal efficiency, ηth, represents the fraction of heat, QH, that is converted to work. Since energy is conserved according to the first law of thermodynamics and energy cannot be be converted to work completely, the heat input, QH, must equal the work done, W, plus the heat that must be dissipated as waste heat QC into the environment. Therefore we can rewrite the formula for thermal efficiency as:

thermal efficiency formula - 2

The heat absorbed occurs during combustion of fuel-air mixture, when the spark occurs, roughly at constant volume. Since during an isochoric process there is no work done by or on the system, the first law of thermodynamics dictates ∆U = ∆Q. Therefore the heat added and rejected are given by:

Qadd = mcv (T3 – T2)

Qout = mcv (T4 – T1)

Substituting these expressions for the heat added and rejected in the expression for thermal efficiency yields:

Otto cycle - efficiency - equation

We can simplify the above expression using the fact that the processes 1 → 2 and from 3 → 4 are adiabatic and for an adiabatic process the following p,V,T formula is valid:

adiabatic process - formula

It can be derived that:

adiabatic process - formula2

In this equation, the ratio V1/V2 is known as the compression ratio, CR. When we rewrite the expression for thermal efficiency using the compression ratio, we conclude the air-standard Otto cycle thermal efficiency is a function of compression ratio and κ = cp/cv.

thermal efficiency - Otto Cycle - Compression ratio

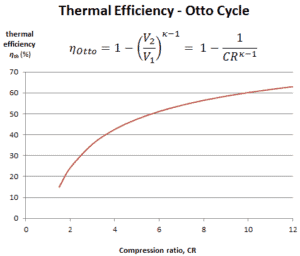
thermal efficiency - Otto Cycle - Engine
Thermal efficiency for Otto cycle – κ = 1.4

It is very useful conclusion, because it is desirable to achieve a high compression ratio to extract more mechanical energy from a given mass of air-fuel mixture. A higher compression ratio permit the same combustion temperature to be reached with less fuel, while giving a longer expansion cycle. This creates more mechanical power output and lowers the exhaust temperature. Lowering the exhaust temperature causes the lowering of the energy rejected to the atmosphere. This relationship is shown in the figure for κ = 1.4, representing ambient air.

 
Efficiency of Engines in Transportation
  • In the middle of twentieth century, a typical steam locomotive had a thermal efficiency of about 6%. That means for every 100 MJ of coal burned, 6 MJ of mechanical power were produced.
  • A typical gasoline automotive engine operates at around 25% to 30% of thermal efficiency. About 70-75% is rejected as waste heat without being converted into useful work, i.e. work delivered to wheels.
  • A typical diesel automotive engine operates at around 30% to 35%. In general, engines using the Diesel cycle are usually more efficient.
  • In 2014, new regulations were introduced for Formula 1 cars. These motorsport regulations have pushed teams to develop highly efficient power units. According to Mercedes, their power unit is now achieving more than 45% and close to 50% thermal efficiency, i.e. 45 – 50% of the potential energy in the fuel is delivered to wheels.
  • The diesel engine has the highest thermal efficiency of any practical combustion engine. Low-speed diesel engines (as used in ships) can have a thermal efficiency that exceeds 50%. The largest diesel engine in the world peaks at 51.7%.

Compression Ratio – Otto Engine

The compression ratio, CR, is defined as the ratio of the volume at bottom dead center and the volume at top dead center.  It is a key characteristics for many internal combustion engines. In the following section, it will be shown that the compression ratio determines the thermal efficiency of used thermodynamic cycle of the combustion engine. In general, it is desired to have a high compression ratio, because it allows an engine to reach higher thermal efficiency.

For example, let assume an Otto cycle with compression ratio of CR = 10 : 1. The volume of the chamber is 500 cm³ = 500×10-6 m3 (0.5l) prior to the compression stroke. For this engine all required volumes are known:

  • V1 = V4 = Vmax = 500×10-6 m3 (0.5l)
  • V2 = V3 = Vmin = Vmax / CR = 55.56 ×10-6 m3

Note that (Vmax – Vmin) x number of cylinders = total engine displacement.

Examples of Compression Ratios – Gasoline vs. Diesel

  • The compression ratio in a gasoline-powered engine will usually not be much higher than 10:1 due to potential engine knocking (autoignition) and not lower than 6:1.
  • A turbocharged Subaru Impreza WRX has a compression ratio of 8.0:1. In general, a turbocharged or supercharged engines already have compressed air at air intake, therefore they are usually built with lower compression ratio.
  • A stock Honda S2000 engine (F22C1) has a compression ratio of 11.1:1.
  • Some atmospheric sportscar engines can have compression ratio up to 12.5 : 1 (e.g. Ferrari 458 Italia).
  • In 2012, Mazda released new petrol engines under the brand name SkyActiv with a 14:1 compression ratio. To reduce the risk of engine knocking, residual gas is reduced by using 4-2-1 engine exhaust systems, implementing a piston cavity, and optimizing fuel injection.
  • The Diesel engines have the compression ratio that normally exceed 14:1 and ratios over 22:1 are also common.
 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Otto Cycle

We hope, this article, Thermal Efficiency for Otto Cycle, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts