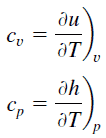Innere Energie eines idealen Gases
Die innere Energie ist die Gesamtenergie, die mit der Bewegung der Atome oder Moleküle im System verbunden ist. Mikroskopische Energieformen umfassen solche, die auf die Rotation , Vibration , Translation und Wechselwirkung zwischen den Molekülen einer Substanz zurückzuführen sind.
Monatomisches Gas – Interne Energie
Für ein einatomiges ideales Gas (wie Helium, Neon oder Argon) kommt der einzige Beitrag zur Energie von der translatorischen kinetischen Energie . Die durchschnittliche translatorische kinetische Energie eines einzelnen Atoms hängt nur von der Gastemperatur ab und wird durch folgende Gleichung angegeben:
K avg = 3/2 kT.
Die innere Energie von n Mol eines idealen einatomigen Gases (ein Atom pro Molekül) entspricht der durchschnittlichen kinetischen Energie pro Molekül multipliziert mit der Gesamtzahl der Moleküle, N:
E int = 3/2 NkT = 3/2 nRT
Dabei ist n die Anzahl der Mole. Jede Richtung (x, y und z) trägt (1/2) nRT zur inneren Energie bei . Hier kommt die Energieausgleichsidee ins Spiel – jeder andere Beitrag zur Energie muss auch (1/2) nRT beitragen . Wie zu sehen ist, hängt die innere Energie eines idealen Gases nur von der Temperatur und der Anzahl der Mol Gas ab.
Diatomic Molecule – Interne Energie
Wenn die Gasmoleküle mehr als ein Atom enthalten, gibt es drei Translationsrichtungen , und die kinetische Rotationsenergie trägt ebenfalls bei, jedoch nur für Rotationen um zwei der drei senkrechten Achsen. Die fünf Beiträge zur Energie (fünf Freiheitsgrade) ergeben:
Diatomeen-Idealgas:
E int = 5/2 NkT = 5/2 nRT
Dies ist nur eine Annäherung und gilt bei Zwischentemperaturen. Bei niedrigen Temperaturen trägt nur die translatorische kinetische Energie bei , und bei höheren Temperaturen kommen zwei zusätzliche Beiträge (kinetische und potentielle Energie) durch Vibration. Die innere Energie ist bei einer gegebenen Temperatur größer als bei einem einatomigen Gas, aber sie ist immer noch nur eine Funktion der Temperatur für ein ideales Gas.
Die innere Energie realer Gase hängt ebenfalls hauptsächlich von der Temperatur ab, aber ähnlich wie das ideale Gasgesetz hängt die innere Energie realer Gase auch etwas von Druck und Volumen ab . Alle realen Gase nähern sich bei niedrigen Drücken (Dichten) dem Idealzustand. Bei niedrigen Drücken sind Moleküle weit genug voneinander entfernt, dass sie nicht miteinander interagieren. Die innere Energie von Flüssigkeiten und Festkörpern ist ziemlich kompliziert, da sie elektrische potentielle Energie enthält, die mit den Kräften (oder chemischen Bindungen ) zwischen Atomen und Molekülen verbunden ist.
Spezifische Wärme bei konstantem Volumen und konstantem Druck
Spezifische Wärme ist eine Eigenschaft in Bezug auf die innere Energie , die für die Thermodynamik sehr wichtig ist. Die intensiven Eigenschaften c v und c p sind für reine, einfache kompressible Substanzen als partielle Ableitungen der inneren Energie u (T, v) bzw. der Enthalpie h (T, p) definiert :
wobei die Indizes v und p die Variablen bezeichnen, die während der Differenzierung festgehalten werden. Die Eigenschaften c v und c p werden als spezifische Wärme (oder Wärmekapazität ) bezeichnet, da sie unter bestimmten besonderen Bedingungen die Temperaturänderung eines Systems mit der durch Wärmeübertragung hinzugefügten Energiemenge in Beziehung setzen. Ihre SI – Einheiten sind J / kg K oder J / mol K . Für Gase sind zwei spezifische Wärmemengen definiert, eine für konstantes Volumen (c v ) und eine für konstanten Druck (c p ) .
Nach dem ersten Hauptsatz der Thermodynamik beträgt für einen Prozess mit konstantem Volumen mit einem einatomigen idealen Gas die molare spezifische Wärme:
C v = 3 / 2R = 12,5 J / mol K.
da
U = 3 / 2nRT
Es kann abgeleitet werden, dass die molare spezifische Wärme bei konstantem Druck ist:
C p = C v + R = 5 / 2R = 20,8 J / mol K.
Dieses C p ist größer als die molare spezifische Wärme bei konstantem Volumen C v , da nun nicht nur Energie zugeführt werden muss , um die Temperatur des Gases zu erhöhen, sondern auch, damit das Gas funktioniert, da sich in diesem Fall das Volumen ändert.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
