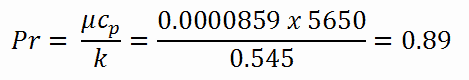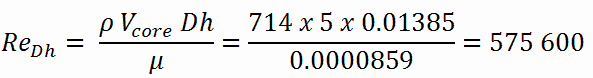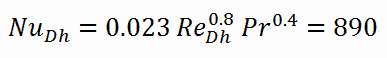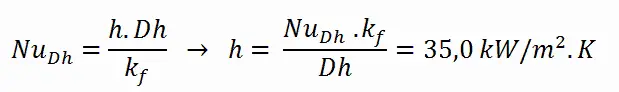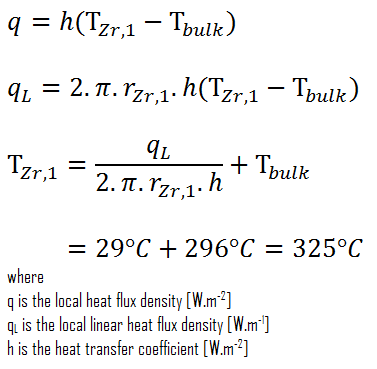Beispiel – Konvektion – Manteloberflächentemperatur
Beispiel – Konvektion – Problem mit Lösung
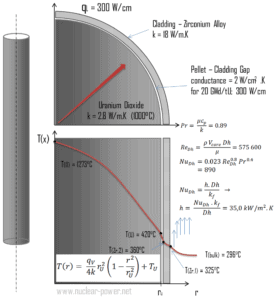
Mantel ist die äußere Schicht der Brennstäbe, die zwischen dem Reaktorkühlmittel und dem Kernbrennstoff(dh Brennstoffpellets ) steht. Es besteht aus einem korrosionsbeständigen Material mit geringem Absorptionsquerschnitt für thermische Neutronen , üblicherweise aus einer Zirkoniumlegierung . Die Ummantelung verhindert, dass radioaktive Spaltprodukte aus der Brennstoffmatrix in das Reaktorkühlmittel gelangen und dieses verunreinigen. Verkleidungen stellen eine der Barrieren bei der Tiefenverteidigung dar , daher ist ihre Kühlbarkeit einer der wichtigsten Sicherheitsaspekte.
Betrachten Sie die Kraftstoffhülle mit dem Innenradius r Zr, 2 = 0,408 cm und dem Außenradius r Zr, 1 = 0,465 cm . Im Vergleich zu Brennstoffpellets entsteht in der Brennstoffhülle kaum Wärme (die Hülle wird durch Strahlung leicht erwärmt ). Die gesamte im Kraftstoff erzeugte Wärme muss durch Leitung durch die Ummantelung übertragen werden, und daher ist die Innenfläche heißer als die Außenfläche.
Annehmen, dass:
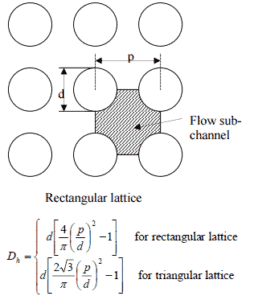
- Der Außendurchmesser der Ummantelung beträgt: d = 2 xr Zr, 1 = 9,3 mm
- Die Steigung der Kraftstoffstifte beträgt: p = 13 mm
- Die Wärmeleitfähigkeit von gesättigtem Wasser bei 300 ° C beträgt: k H 2 O = 0,545 W / mK
- Die dynamische Viskosität von gesättigtem Wasser bei 300 ° C beträgt: μ = 0,0000859 Ns / m 2
- Die Flüssigkeitsdichte beträgt : ρ = 714 kg / m 3
- Die spezifische Wärme beträgt: c p = 5,65 kJ / kg K.
- Die Kernströmungsgeschwindigkeit ist konstant und gleich V Kern = 5 m / s
- Die Temperatur des Reaktorkühlmittels bei dieser axialen Koordinate beträgt: T Volumen = 296 ° C.
- Die lineare Heizrate des Brennstoffs beträgt q L = 300 W / cm (F Q ≤ 2,0) und somit beträgt die volumetrische Heizrate q V = 597 × 10 6 W / m 3
Berechnen Sie die Prandtl , Reynolds und Nusselt – Zahl für dieses Strömungsregime (interne forcierter turbulente Strömung) innerhalb des rechteckigen Brennstoffgitters (Brennstoffkanal), berechnen dann den Wärmeübergangskoeffizienten und schließlich die Manteloberflächentemperatur , T Zr, 1 .
Um die Manteloberflächentemperatur zu berechnen, müssen wir die Prandtl- , Reynolds- und Nusselt-Zahl berechnen , da der Wärmeübergang für dieses Strömungsregime durch die Dittus-Boelter-Gleichung beschrieben werden kann :
Berechnung der Prandtlschen Zahl
Um die Prandtl-Zahl zu berechnen , müssen wir wissen:
- Die Wärmeleitfähigkeit von gesättigtem Wasser bei 300 ° C beträgt: k H 2 O = 0,545 W / mK
- Die dynamische Viskosität von gesättigtem Wasser bei 300 ° C beträgt: μ = 0,0000859 Ns / m 2
- Die spezifische Wärme beträgt: c p = 5,65 kJ / kg K.
Beachten Sie, dass sich alle diese Parameter für Wasser bei 300 ° C erheblich von denen bei 20 ° C unterscheiden. Die Prandtl-Zahl für Wasser bei 20 ° C liegt bei 6,91. Die Prandtl-Zahl für Reaktorkühlmittel bei 300 ° C lautet dann:
Berechnung der Reynoldszahl
Um die Reynolds-Zahl zu berechnen, müssen wir wissen:
- Der Außendurchmesser der Ummantelung beträgt: d = 2 xr Zr, 1 = 9,3 mm (zur Berechnung des hydraulischen Durchmessers)
- Die Steigung der Kraftstoffstifte beträgt: p = 13 mm (zur Berechnung des Hydraulikdurchmessers)
- Die dynamische Viskosität von gesättigtem Wasser bei 300 ° C beträgt: μ = 0,0000859 Ns / m 2
- Die Flüssigkeitsdichte beträgt: ρ = 714 kg / m 3
Der hydraulische Durchmesser D h ist ein häufig verwendeter Begriff bei der Handhabung von Strömungen in nicht kreisförmigen Rohren und Kanälen . Der hydraulische Durchmesser des Brennstoffkanals , D h , ist auf 13,85 mm.
Siehe auch: Hydraulikdurchmesser
Die Reynolds-Zahl innerhalb des Kraftstoffkanals ist dann gleich:
Dies erfüllt die turbulenten Bedingungen vollständig .
Berechnung der Nusselt-Zahl nach Dittus-Boelter-Gleichung
Für eine vollständig entwickelte (hydrodynamisch und thermisch) turbulente Strömung in einem glatten kreisförmigen Rohr kann die lokale Nusselt-Zahl aus der bekannten Dittus-Boelter-Gleichung erhalten werden .
Um die Nusselt-Zahl zu berechnen , müssen wir wissen:
- die Reynolds-Zahl , die Re Dh = 575600 ist
- die Prandtl-Zahl , die Pr = 0,89 ist
Die Nusselt-Zahl für die erzwungene Konvektion innerhalb des Kraftstoffkanals ist dann gleich:
Berechnung des Wärmeübergangskoeffizienten und der Manteloberflächentemperatur, T Zr, 1
Detaillierte Kenntnisse der Geometrie, der Fluidparameter, des Außenmantelradius, der linearen Heizrate und des konvektiven Wärmeübertragungskoeffizienten ermöglichen die Berechnung der Temperaturdifferenz ∆T zwischen dem Kühlmittel (T- Volumen ) und der Manteloberfläche (T Zr, 1 ).
Um die Plattentemperatur zu berechnen, müssen wir wissen:
- der Außendurchmesser der Ummantelung beträgt: d = 2 x r Zr, 1 = 9,3 mm
- die Nusselt-Zahl, die Nu Dh = 890 ist
- Der hydraulische Durchmesser des Kraftstoffkanals beträgt: D h = 13,85 mm
- Die Wärmeleitfähigkeit des Reaktorkühlmittels (300 ° C) beträgt: k H 2 O = 0,545 W / mK
- Die Massentemperatur des Reaktorkühlmittels bei dieser axialen Koordinate beträgt: T Volumen = 296 ° C.
- Die lineare Heizrate des Brennstoffs beträgt: q L = 300 W / cm (F Q ≈ 2,0)
Der konvektive Wärmeübergangskoeffizient h wird direkt durch die Definition der Nusselt-Zahl angegeben:
Schließlich können wir die Temperatur der Manteloberfläche (T Zr, 1 ) einfach nach dem Newtonschen Gesetz der Kühlung berechnen :
Bei PWRs im Normalbetrieb befindet sich im Reaktorkern, in den Kreisläufen und in den Dampferzeugern komprimiertes flüssiges Wasser . Der Druck wird bei ungefähr 16 MPa gehalten . Bei diesem Druck kocht Wasser bei ungefähr 350 ° C (662 ° F). Wie zu sehen ist, stellt die Oberflächentemperatur T Zr, 1 = 325 ° C sicher, dass auch unterkühltes sieden nicht auftritt. Es ist zu beachten, dass unterkühltes sieden T Zr erfordert , 1 = T sat . Da die Einlasstemperaturen des Wassers üblicherweise ca. 290 ° C betragen(554 ° F) ist es offensichtlich, dass dieses Beispiel dem unteren Teil des Kerns entspricht. In höheren Lagen des Kerns kann die Massentemperatur bis zu 330 ° C erreichen. Der Temperaturunterschied von 29 ° C führt dazu, dass unterkühltes sieden auftreten kann (330 ° C + 29 ° C> 350 ° C). Andererseits stört das sieden von Keimen an der Oberfläche die stagnierende Schicht effektiv, und daher erhöht das sieden von Keimen die Fähigkeit einer Oberfläche, Wärmeenergie auf Schüttgut zu übertragen, erheblich . Infolgedessen steigt der konvektive Wärmeübergangskoeffizient signifikant an und daher nimmt in höheren Lagen die Temperaturdifferenz (T Zr, 1 – T Volumen ) signifikant ab.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
