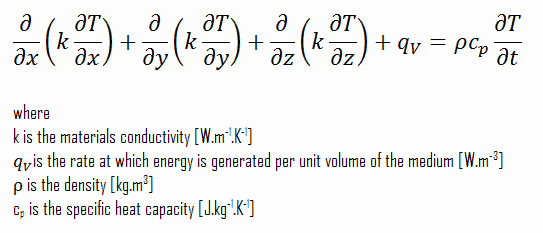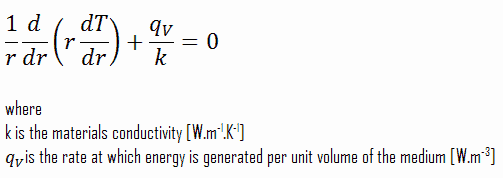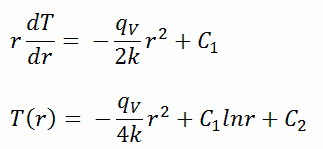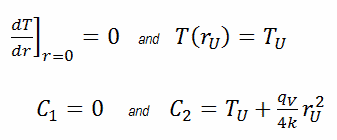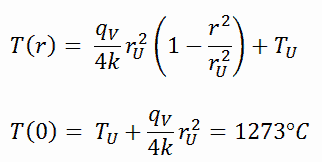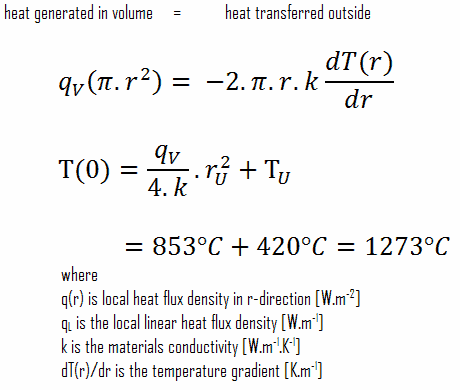Was ist Wärmeleitung – Wärmeleitung – Definition

Wärmeleitung – Wärmeleitung

Die Wärmeleitung , auch Wärmeleitung genannt , findet innerhalb eines Körpers oder zwischen zwei sich berührenden Körpern statt, ohne dass Massenstrom und Vermischung beteiligt sind. Es ist der direkte mikroskopische Austausch der kinetischen Energie von Partikeln durch die Grenze zwischen zwei Systemen. Die Wärmeübertragung durch Wärmeleitung ist abhängig von der treibenden „Kraft“ der Temperaturdifferenz und der Wärmeleitfähigkeit (oder dem Widerstand gegen die Wärmeübertragung). Die Wärmeleitfähigkeit ist abhängig von der Art und den Abmessungen des Wärmeträgers. Alle Wärmeübertragungsprobleme betreffen die Temperaturdifferenz , die Geometrieund die physikalischen Eigenschaften des zu untersuchenden Objekts. Bei Problemen mit der Wärmeleitung ist das zu untersuchende Objekt normalerweise ein Feststoff.

Mikroskopisch wird diese Art des Energietransfers dem freien Elektronenfluss von höheren zu niedrigeren Energieniveaus, der Gittervibration und der molekularen Kollision zugeschrieben .  Stellen Sie sich einen Steinblock mit hoher Temperatur vor, der aus Atomen besteht, die stark um ihre durchschnittliche Position schwingen. Bei niedrigen Temperaturen schwingen die Atome weiter, jedoch mit geringerer Intensität .Wenn ein heißerer Steinblock mit einem kühleren Block in Kontakt gebracht wird, geben die stark schwingenden Atome am Rand des heißeren Blocks ihre kinetische Energie an die weniger schwingenden Atome am Rand des kühlen Blocks ab. In diesem Fall findet zwischen diesen beiden Blöcken ein Energietransfer statt , und durch diese zufälligen Vibrationen fließt Wärme vom heißeren zum kühleren Block. Die moderne Sichtweise besteht darin, den Energietransfer Gitterwellen zuzuschreiben, die durch atomare Bewegung induziert werden. Bei einem elektrischen Isolator erfolgt die Energieübertragung ausschließlich über diese Gitterwellen. In einem Leiter liegt es auch an der Translationsbewegung der freien Elektronen.

Siehe auch: Zeroth-Gesetz der Thermodynamik

Im Allgemeinen Metalle sind in der Regel guter Leiter von Wärmeenergie . Es ist eng mit seiner guten elektrischen Leitfähigkeit verbunden . Bei Metallen ist die Wärmeleitfähigkeit recht hoch, und diejenigen Metalle, die die besten elektrischen Leiter sind, sind auch die besten Wärmeleiter. Dies liegt an der chemischen Bindung der Metalle. Metallische Bindungen haben frei bewegliche Elektronen (freie Elektronen), die Wärmeenergie schnell durch das Metall übertragen. Das Elektronenfluid eines leitenden metallischen Feststoffs leitet den größten Teil des Wärmeflusses durch den Feststoff. Der Phononenfluss ist immer noch vorhanden, trägt aber weniger Energie. Diese Mechanismen der Wärmeleitung werden später diskutiert.

Fourier’sches Wärmeleitungsgesetz

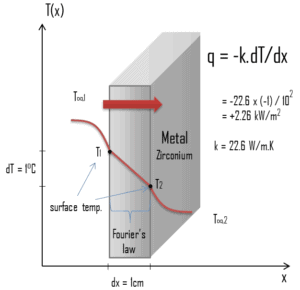
Wärmeübertragungsprozesse können durch geeignete Ratengleichungen quantifiziert werden. Die Geschwindigkeitsgleichung in diesem Wärmeübertragungsmodus basiert auf dem Fourierschen Wärmeleitungsgesetz . Dieses Gesetz besagt, dass die Zeitrate der Wärmeübertragung durch ein Material proportional zu dem negativen Temperaturgradienten und zu der Fläche ist, die rechtwinklig zu dem Gradienten verläuft, durch den die Wärme fließt. Ihre Differentialform ist:

Ähnlich wie das Fourier-Gesetz den Wärmefluss durch eine Platte bestimmt, kann es auch verwendet werden, um die Temperaturdifferenz zu bestimmen, wenn q bekannt ist. Dies kann zur Berechnung der Temperatur in der Mitte des Brennstoffpellets verwendet werden, wie in den folgenden Abschnitten gezeigt wird.

Wärmeleitungsgleichung

In früheren Abschnitten haben wir uns insbesondere mit der eindimensionalen Wärmeübertragung im stationären Zustand befasst, die durch das Fourier-Gesetz der Wärmeleitung charakterisiert werden kann . Ihre Anwendbarkeit ist jedoch sehr begrenzt. Dieses Gesetz geht von einer stationären Wärmeübertragung durch einen planaren Körper aus (beachten Sie, dass das Fourier-Gesetz auch für Zylinder- und Kugelkoordinaten abgeleitet werden kann), ohne Wärmequellen . Es ist einfach die Geschwindigkeitsgleichung in diesem Wärmeübertragungsmodus, in dem der Temperaturgradient bekannt ist.

Ein Hauptproblem bei den meisten Leitungsanalysen besteht jedoch darin, das Temperaturfeld in einem Medium zu bestimmen, das sich aus den an seine Grenzen auferlegten Bedingungen ergibt. In der Technik müssen wir Wärmeübertragungsprobleme lösen, die unterschiedliche Geometrien und Bedingungen betreffen, wie z. B. ein zylindrisches Kernbrennelement, bei dem es sich um eine interne Wärmequelle oder die Wand eines kugelförmigen Containments handelt. Diese Probleme sind komplexer als die planaren Analysen, die wir in den vorherigen Abschnitten durchgeführt haben. Daher werden diese Probleme Gegenstand dieses Abschnitts sein, in dem die Wärmeleitungsgleichung eingeführt und gelöst wird.

Siehe auch: Wärmegleichung

Wärmeleitungsgleichung – Allgemeine Form

Die Wärmeleitungsgleichung ist eine partielle Differentialgleichung, die die Verteilung der Wärme (oder des Temperaturfeldes ) in einem bestimmten Körper über die Zeit beschreibt. Detaillierte Kenntnisse des Temperaturfeldes sind für die Wärmeleitung durch Materialien sehr wichtig. Sobald diese Temperaturverteilung bekannt ist, kann der Wärmeleitungsfluss an jedem Punkt im Material oder auf seiner Oberfläche nach dem Fourier-Gesetz berechnet werden .

Die Wärmegleichung leitet sich aus dem Fourier-Gesetz und der Energieerhaltung ab . Das Fourier-Gesetz besagt, dass die zeitliche Wärmeübertragungsrate durch ein Material proportional zum negativen Temperaturgradienten und zu der Fläche im rechten Winkel zu dem Gradienten ist, durch den die Wärme fließt.

Eine Änderung der inneren Energie pro Volumeneinheit im Material ΔQ ist proportional zur Änderung der Temperatur Δu. Das ist:

∆Q = ρ.c _p .∆T

Generelle Form

Unter Verwendung dieser beiden Gleichungen können wir die allgemeine Wärmeleitungsgleichung ableiten:

Diese Gleichung wird auch als Fourier-Biot-Gleichung bezeichnet und bietet das grundlegende Werkzeug für die Wärmeleitungsanalyse. Aus seiner Lösung können wir das Temperaturfeld als Funktion der Zeit erhalten.

In Worten heißt es in der Wärmeleitungsgleichung :

Zu jedem Zeitpunkt im Medium muss die Nettorate der Energieübertragung durch Leitung in ein Volumeneinheit plus die Volumenrate der Wärmeenergieerzeugung gleich der Änderungsrate der im Volumen gespeicherten Wärmeenergie sein.

Siehe auch: Wärmeleitfähigkeit

Beispiel – Wärmeleitung im Brennstab

Die meisten PWRs verwenden den Uranbrennstoff , der in Form von Urandioxid vorliegt . Urandioxid ist ein schwarzer halbleitender Feststoff mit sehr geringer Wärmeleitfähigkeit. Andererseits hat das Urandioxid einen sehr hohen Schmelzpunkt und ein bekanntes Verhalten. Das UO ₂ wird zu zylindrischen Pellets gepresst , diese Pellets werden dann in den Feststoff gesintert.

Diese zylindrischen Pellets werden dann in einem Brennstab (oder Brennstoff pin) geladen und eingekapselt, die aus Zirconium – Legierungen sind aufgrund seines sehr geringen Absorptionsquerschnittes (im Unterschied zu dem rostfreien Stahl). Die Oberfläche des Rohrs, die die Pellets bedeckt, wird als Brennstoffmantel bezeichnet .

Siehe auch:  Wärmeleitung von Urandioxid

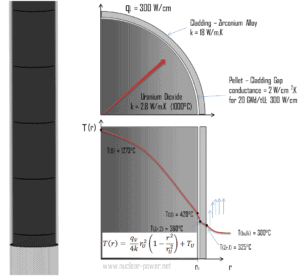
Das thermische und mechanische Verhalten von Brennstoffpellets  und Brennstäben bildet eine von drei zentralen Konstruktionsdisziplinen. Kernbrennstoff wird unter sehr unwirtlichen Bedingungen (thermisch, strahlend, mechanisch) betrieben und muss mehr als normalen Betriebsbedingungen standhalten. Beispielsweise erreichen die Temperaturen in der Mitte von Brennstoffpellets mehr als 1000 ° C (1832 ° F), begleitet von Spaltgasfreisetzungen. Daher ist eine detaillierte Kenntnis der Temperaturverteilung innerhalb eines einzelnen Brennstabs für den sicheren Betrieb von Kernbrennstoff unerlässlich. In diesem Abschnitt werden wir die Wärmeleitungsgleichung in Zylinderkoordinaten untersuchenunter Verwendung der Dirichlet-Randbedingung bei gegebener Oberflächentemperatur (dh unter Verwendung der Dirichlet-Randbedingung). Eine umfassende Analyse des Brennstabtemperaturprofils wird in einem separaten Abschnitt untersucht.

Temperatur in der Mittellinie eines Brennstoffpellets

Betrachten Sie das Brennstoffpellet mit dem Radius r _U = 0,40 cm , bei dem eine gleichmäßige und konstante Wärmeerzeugung pro Volumeneinheit q _V [W / m ³ ] erfolgt . Anstelle der volumetrischen Heizrate q _V [W / m ³ ] verwenden Ingenieure häufig die lineare Heizrate q _L [W / m] , die die Heizrate eines Meters Brennstab darstellt. Die lineare Heizrate kann aus der volumetrischen Heizrate berechnet werden durch:

Die Mittellinie wird als Ursprung für die r-Koordinate verwendet. Aufgrund der Symmetrie in z-Richtung und in azimutaler Richtung können wir Variablen trennen und dieses Problem zu einem eindimensionalen Problem vereinfachen . Wir werden also nur nach der Temperatur als Funktion des Radius T (r) suchen. Für eine konstante Wärmeleitfähigkeit ist k, die geeignete Form der zylindrischen Wärmegleichung ,:

Die allgemeine Lösung dieser Gleichung lautet:

wobei C ₁ und C ₂ die Integrationskonstanten sind.

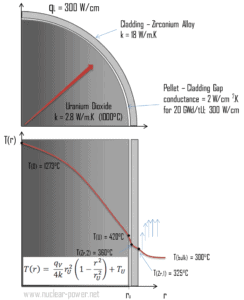Berechnen Sie die Temperaturverteilung T (r) in diesem Brennstoffpellet, wenn:

• Die Temperaturen an der Oberfläche des Brennstoffpellets betragen T _U = 420 ° C.
• der Brennstoffpelletradius r _U = 4 mm .
• Die Leitfähigkeit des gemittelten Materials beträgt k = 2,8 W / mK (entspricht Urandioxid bei 1000 ° C).
• Die lineare Heizrate beträgt q _L = 300 W / cm und somit beträgt die volumetrische Heizrate q _V = 597 × 10 ⁶ W / m ³

In diesem Fall wird die Oberfläche bei gegebenen Temperaturen T _{U gehalten} . Dies entspricht der Dirichlet-Randbedingung . Darüber hinaus ist dieses Problem thermisch symmetrisch und daher können wir auch die thermische Symmetrie-Randbedingung verwenden . Die Konstanten können durch Substitution in die allgemeine Lösung bewertet werden und haben die Form:

Die resultierende Temperaturverteilung und die Mittellinientemperatur (r = 0) (maximal) in diesem zylindrischen Brennstoffpellet bei diesen spezifischen Randbedingungen sind:

Der radiale Wärmefluss bei jedem Radius q _r [Wm ^-1 ] im Zylinder kann natürlich unter Verwendung der Temperaturverteilung und nach dem Fourier-Gesetz bestimmt werden . Beachten Sie, dass mit der Wärmeerzeugung der Wärmefluss nicht mehr unabhängig von r ist.

∆T im Brennstoffpellet

Detaillierte Kenntnisse der Geometrie, des Außenradius des Brennstoffpellets, der volumetrischen Heizrate und der Pelletoberflächentemperatur (T _U ) bestimmen ∆T zwischen der Außenfläche und der Mittellinie des Brennstoffpellets. Daher können wir die Mittellinientemperatur (T _{Zr, 2} ) einfach anhand der Energieeinsparung zwischen der im Volumen erzeugten Wärme und der außerhalb des Volumens übertragenen Wärme berechnen :

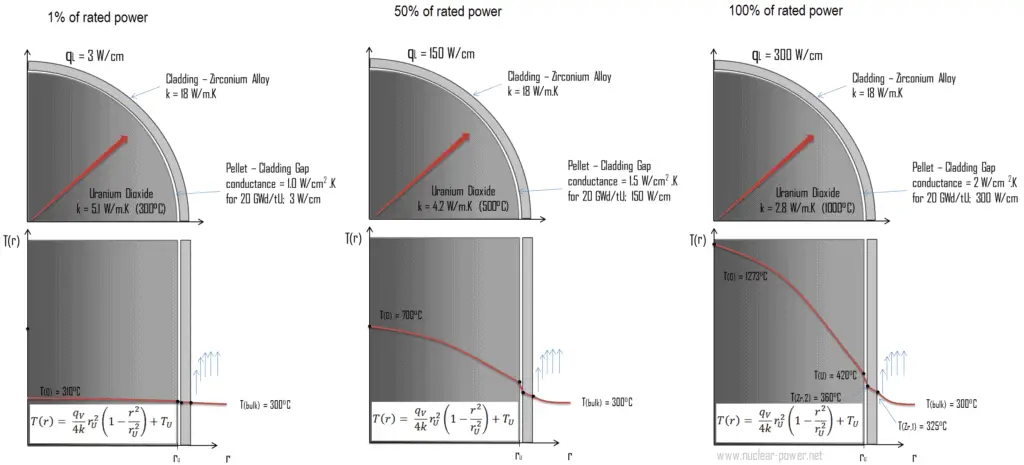
Die folgende Abbildung zeigt die Temperaturverteilung im Brennstoffpellet bei verschiedenen Leistungsstufen.

______

Die Temperatur in einem Betriebsreaktor variiert von Punkt zu Punkt innerhalb des Systems. Infolgedessen gibt es immer einen Brennstab und ein lokales Volumen , die heißer sind  als alle anderen. Um diese heißen Orte zu begrenzen, müssen die Spitzenleistungsgrenzen eingeführt werden. Die Spitzenleistungsgrenzen sind mit einer Siedekrise und mit den Bedingungen verbunden, die eine Brennstoffpelletschmelze verursachen können. Metallurgische Überlegungen begrenzen jedoch die Temperatur des Brennstoffmantels und des Brennstoffpellets nach oben. Über diesen TemperaturenEs besteht die Gefahr, dass der Kraftstoff beschädigt wird. Eines der Hauptziele bei der Auslegung eines Kernreaktors besteht darin, die Wärmeabfuhr bei der gewünschten Leistung zu gewährleisten und gleichzeitig sicherzustellen, dass die maximale Brennstofftemperatur und die maximale Plattiertemperatur immer unter diesen vorgegebenen Werten liegen.