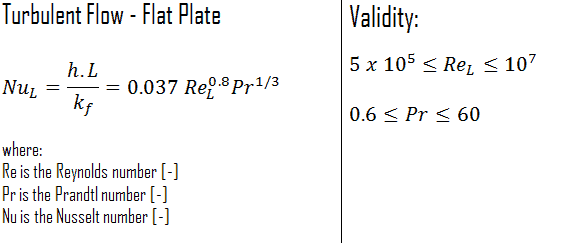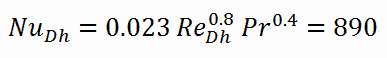Klassifizierung von Strömungsregimen
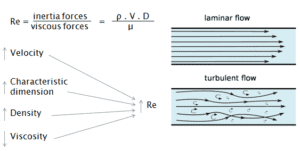Eine weitere häufigere Klassifizierung von Strömungsregimen erfolgt nach Form und Art der Stromlinien . Der gesamte Flüssigkeitsstrom wird in eine von zwei großen Kategorien eingeteilt. Die Fluidströmung kann entweder laminar oder turbulent sein, und daher sind diese beiden Kategorien:
Laminare Strömung ist gekennzeichnet durch glatte oder in regelmäßigen Bahnen befindliche Partikel der Flüssigkeit. Daher wird die laminare Strömung auch als Stromlinien- oder viskose Strömung bezeichnet . Im Gegensatz zur laminaren Strömung ist die turbulente Strömung durch die unregelmäßige Bewegung von Flüssigkeitsteilchen gekennzeichnet. Das turbulente Fluid fließt nicht in parallelen Schichten, die seitliche Vermischung ist sehr hoch und es kommt zu einer Störung zwischen den Schichten. Die meisten industriellen Strömungen , insbesondere in der Kerntechnik, sind turbulent .
Laminare Strömung
In der Fluiddynamik ist die laminare Strömung durch glatte oder regelmäßige Wege von Fluidpartikeln gekennzeichnet, im Gegensatz zur turbulenten Strömung, die durch die unregelmäßige Bewegung von Fluidpartikeln gekennzeichnet ist. Die Flüssigkeit fließt in parallelen Schichten (mit minimaler seitlicher Vermischung) ohne Unterbrechung zwischen den Schichten. Daher wird die laminare Strömung auch als stromlinienförmige oder viskose Strömung bezeichnet .
Der Begriff Stromlinienströmung beschreibt die Strömung, da bei laminarer Strömung Wasserschichten mit unterschiedlichen Geschwindigkeiten übereinander fließen und sich praktisch nicht zwischen den Schichten vermischen. Fluidpartikel bewegen sich auf bestimmten und beobachtbaren Wegen oder Stromlinien.
Wenn ein Fluid durch einen geschlossenen Kanal wie ein Rohr oder zwischen zwei flachen Platten fließt, kann abhängig von der Geschwindigkeit , der Viskosität des Fluids und der Größe des Rohrs eine von zwei Strömungsarten (laminare Strömung oder turbulente Strömung) auftreten . Laminare Strömung tritt tendenziell bei niedrigeren Geschwindigkeiten und hoher Viskosität auf . Andererseits tritt eine turbulente Strömung tendenziell bei höheren Geschwindigkeiten und niedriger Viskosität auf.
Da laminare Strömung nur in Fällen üblich ist, in denen der Strömungskanal relativ klein ist, sich das Fluid langsam bewegt und seine Viskosität relativ hoch ist, ist laminare Strömung in industriellen Prozessen nicht üblich. Die meisten industriellen Strömungen, insbesondere in der Nukleartechnik, sind turbulent. Trotzdem tritt eine laminare Strömung bei jeder Reynolds-Zahl in der Nähe fester Grenzen in einer dünnen Schicht direkt neben der Oberfläche auf. Diese Schicht wird üblicherweise als laminare Unterschicht bezeichnet und ist für die Wärmeübertragung sehr wichtig.
Siehe auch: Reynolds-Nummer
Siehe auch: Kritische Reynoldszahl
Externe laminare Strömung – Nusselt-Zahl
Die durchschnittliche Nusselt-Zahl über die gesamte Platte wird bestimmt durch:
Diese Beziehung gibt den durchschnittlichen Wärmeübergangskoeffizienten für die gesamte Platte an, wenn die Strömung über die gesamte Platte laminar ist.
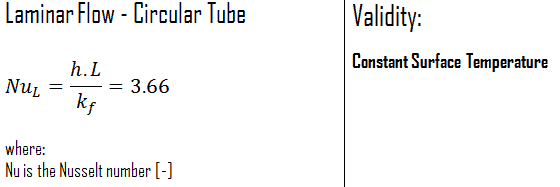
Interne laminare Strömung – Nusselt-Zahl
Konstante Oberflächentemperatur
Bei laminarer Strömung in einem Rohr mit konstanter Oberflächentemperatur bleiben sowohl der Reibungsfaktor als auch der Wärmeübergangskoeffizient im voll entwickelten Bereich konstant.
Konstanter Oberflächenwärmestrom
Daher ist für voll entwickelten laminare Strömung in einem kreisförmigen Rohr konstanten Oberflächen unterworfen Wärmefluss ist die Nusselt – Zahl eine Konstante. Es besteht keine Abhängigkeit von den Reynolds- oder Prandtl-Zahlen .
Turbulente Strömung
In der Fluiddynamik ist eine turbulente Strömung durch die unregelmäßige Bewegung von Partikeln (man kann sagen chaotisch ) des Fluids gekennzeichnet. Im Gegensatz zur laminaren Strömung fließt die Flüssigkeit nicht in parallelen Schichten, die seitliche Vermischung ist sehr hoch und es gibt eine Störung zwischen den Schichten. Turbulenzen sind auch durch Rezirkulation, Wirbel und offensichtliche Zufälligkeit gekennzeichnet . Bei turbulenter Strömung ändert sich die Geschwindigkeit des Fluids an einem Punkt kontinuierlich sowohl in der Größe als auch in der Richtung.
Die detaillierte Kenntnis des Verhaltens der turbulenten Strömungsregime ist von Bedeutung in der Technik, weil die meisten Industrieströme , vor allem in der Kerntechnik sind turbulent . Leider erschwert der stark intermittierende und unregelmäßige Charakter von Turbulenzen alle Analysen . Tatsächlich wird Turbulenzen oft als das „letzte ungelöste Problem in der klassischen mathematischen Physik“ bezeichnet.
Das Hauptwerkzeug für ihre Analyse ist die CFD-Analyse . CFD ist ein Zweig der Strömungsmechanik, der numerische Analysen und Algorithmen verwendet, um Probleme mit turbulenten Strömungen zu lösen und zu analysieren. Es ist allgemein anerkannt, dass die Navier-Stokes-Gleichungen (oder vereinfachte Reynolds-gemittelte Navier-Stokes-Gleichungen ) turbulente Lösungen aufweisen können, und diese Gleichungen bilden die Grundlage für im Wesentlichen alle CFD-Codes.
Externe turbulente Strömung – Nusselt-Zahl
Die durchschnittliche Nusselt-Zahl über die gesamte Platte wird bestimmt durch:
Diese Beziehung gibt den durchschnittlichen Wärmeübergangskoeffizienten für die gesamte Platte nur dann an, wenn die Strömung über die gesamte Platte turbulent ist oder wenn der laminare Strömungsbereich der Platte relativ zum turbulenten Strömungsbereich zu klein ist.
Interne turbulente Strömung – Nusselt-Zahl
Siehe auch: Dittus-Boelter-Gleichung
Für eine vollständig entwickelte (hydrodynamisch und thermisch) turbulente Strömung in einem glatten kreisförmigen Rohr kann die lokale Nusselt-Zahl aus der bekannten Dittus-Boelter-Gleichung erhalten werden . Die Dittus ?? Boelter-Gleichung ist leicht zu lösen, jedoch weniger genau, wenn ein großer Temperaturunterschied zwischen den Flüssigkeiten besteht, und für raue Rohre (viele kommerzielle Anwendungen) weniger genau, da sie auf glatte Rohre zugeschnitten ist.
Die Dittus-Boelter-Korrelation kann für kleine bis mäßige Temperaturunterschiede T wall – T avg verwendet werden , wobei alle Eigenschaften bei einer gemittelten Temperatur T avg bewertet werden .
Bei Strömungen, die durch große Eigenschaftsschwankungen gekennzeichnet sind, müssen beispielsweise die Korrekturen (z. B. ein Viskositätskorrekturfaktor μ / μ Wand ) berücksichtigt werden, wie von Sieder und Tate empfohlen.
Berechnung der Nusselt-Zahl nach Dittus-Boelter-Gleichung
Für eine vollständig entwickelte (hydrodynamisch und thermisch) turbulente Strömung in einem glatten kreisförmigen Rohr kann die lokale Nusselt-Zahl aus der bekannten Dittus-Boelter-Gleichung erhalten werden .
Um die Nusselt-Zahl zu berechnen , müssen wir wissen:
- die Reynolds-Zahl , die Re Dh = 575600 ist
- die Prandtl-Zahl , die Pr = 0,89 ist
Die Nusselt-Zahl für die erzwungene Konvektion innerhalb des Kraftstoffkanals ist dann gleich:
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
