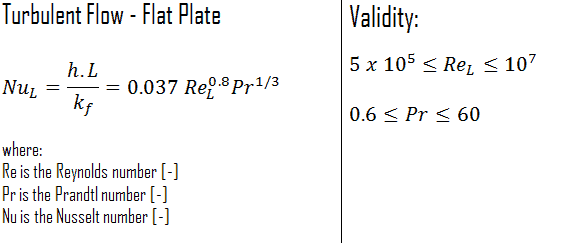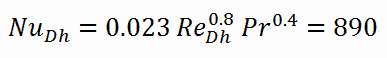Classification des régimes d’écoulement
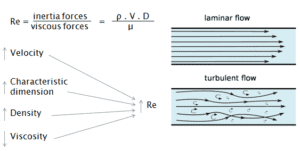Une autre classification des régimes d’écoulement, généralement plus courante, est la forme et le type des lignes de courant . Tout écoulement de fluide est classé dans l’une des deux grandes catégories. Le flux de fluide peut être laminaire ou turbulent. Ces deux catégories sont donc les suivantes:
Écoulement laminaire est caractérisé par lisse ou dans des chemins réguliers de particules de fluide. Par conséquent, l’écoulement laminaire est également appelé écoulement fluide ou visqueux . Contrairement à l’écoulement laminaire, l’écoulement turbulent est caractérisé par le mouvement irrégulier des particules du fluide. Le fluide turbulent ne coule pas dans les couches parallèles, le mélange latéral est très élevé et il y a une rupture entre les couches. La plupart des flux industriels , notamment ceux du génie nucléaire, sont turbulents .
Écoulement laminaire
Dans la dynamique des fluides, l’écoulement laminaire est caractérisé par des trajectoires régulières ou régulières des particules du fluide, contrairement à l’écoulement turbulent, qui est caractérisé par le mouvement irrégulier des particules du fluide. Le fluide s’écoule en couches parallèles (avec un mélange latéral minimal), sans interruption entre les couches. Par conséquent, le flux laminaire est également appelé flux simplifié ou flux visqueux .
Le terme écoulement aérodynamique est descriptif de l’écoulement car, dans un écoulement laminaire, des couches d’eau s’écoulant les unes sur les autres à des vitesses différentes sans pratiquement aucun mélange entre les couches, les particules fluides se déplacent selon des trajectoires ou des lignes de courant définies et observables.
Lorsqu’un fluide s’écoule à travers un canal fermé tel qu’un tuyau ou entre deux plaques plates, l’un ou l’autre des deux types de flux (flux laminaire ou flux turbulent) peut se produire en fonction de la vitesse , de la viscosité du fluide et de la taille du tuyau . L’écoulement laminaire a tendance à se produire à des vitesses plus faibles et à une viscosité élevée . D’un autre côté, un écoulement turbulent a tendance à se produire à des vitesses plus élevées et à une faible viscosité.
Puisque l’écoulement laminaire n’est courant que dans les cas où le canal d’écoulement est relativement petit, le fluide se déplace lentement et sa viscosité est relativement élevée, l’écoulement laminaire n’est pas courant dans les processus industriels. La plupart des flux industriels, en particulier ceux du génie nucléaire, sont turbulents. Néanmoins, l’écoulement laminaire se produit à n’importe quel nombre de Reynolds près des limites solides dans une couche mince juste adjacente à la surface, cette couche est généralement appelée sous- couche laminaire et elle est très importante dans le transfert de chaleur.
Voir aussi: Nombre de Reynolds
Voir aussi: Nombre de Reynolds critique
Écoulement laminaire externe – nombre de Nusselt
Le nombre moyen de Nusselt sur toute la plaque est déterminé par:
Cette relation donne le coefficient de transfert de chaleur moyen pour toute la plaque lorsque le flux est laminaire sur toute la plaque.
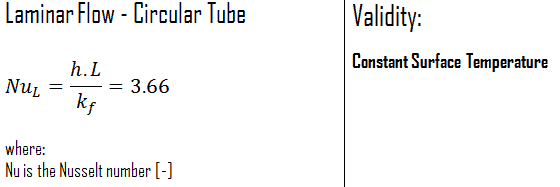
Écoulement laminaire interne – nombre de Nusselt
Température de surface constante
Dans un écoulement laminaire dans un tube à température de surface constante, le facteur de friction et le coefficient de transfert de chaleur restent constants dans la région complètement développée.
Flux de chaleur de surface constant
Par conséquent, pour un écoulement laminaire pleinement développé dans un tube circulaire soumis à un flux thermique de surface constant , le nombre de Nusselt est une constante. Il n’y a aucune dépendance sur les nombres de Reynolds ou de Prandtl .
Écoulement turbulent
En dynamique des fluides, l’ écoulement turbulent est caractérisé par le mouvement irrégulier des particules (on peut dire chaotique ) du fluide. Contrairement au flux laminaire, le fluide ne coule pas en couches parallèles, le mélange latéral est très élevé et il y a une rupture entre les couches. La turbulence est également caractérisée par la recirculation, les tourbillons et le caractère aléatoire apparent . Dans un écoulement turbulent, la vitesse du fluide en un point subit continuellement des changements d’amplitude et de direction.
Une connaissance détaillée du comportement du régime d’écoulement turbulent est importante en génie, car la plupart des écoulements industriels , en particulier ceux du génie nucléaire, sont turbulents . Malheureusement, le caractère hautement intermittent et irrégulier des turbulences complique toutes les analyses . En fait, la turbulence est souvent considérée comme le «dernier problème non résolu de la physique mathématique classique».
Le principal outil disponible pour leur analyse est l’ analyse CFD . CFD est une branche de la mécanique des fluides qui utilise l’analyse numérique et des algorithmes pour résoudre et analyser les problèmes impliquant des écoulements de fluide turbulents. Il est largement admis que les équations de Navier-Stokes (ou les équations simplifiées de Navier-Stokes moyennées par Reynolds ) sont capables de présenter des solutions turbulentes, et ces équations sont la base de pratiquement tous les codes CFD.
Débit turbulent externe – nombre de Nusselt
Le nombre moyen de Nusselt sur toute la plaque est déterminé par:
Cette relation donne le coefficient de transfert thermique moyen pour la plaque entière uniquement lorsque l’écoulement est turbulent sur toute la plaque, ou lorsque la région d’ écoulement laminaire de la plaque est trop petite par rapport à la région d’écoulement turbulent.
Débit turbulent interne – nombre de Nusselt
Voir aussi: Équation Dittus-Boelter
Pour un écoulement turbulent complètement développé (hydrodynamiquement et thermiquement) dans un tube circulaire lisse, le nombre de Nusselt local peut être obtenu à partir de l’ équation bien connue de Dittus-Boelter . L’ équation Dittus ?? Boelter est facile à résoudre mais est moins précise lorsqu’il existe une grande différence de température à travers le fluide et est moins précise pour les tubes rugueux (de nombreuses applications commerciales), car elle est adaptée aux tubes lisses.
La corrélation Dittus-Boelter peut être utilisée pour des différences de température petites à modérées, paroi T – T moyenne , toutes les propriétés étant évaluées à une température moyenne T moyenne .
Pour les flux caractérisés par de grandes variations de propriétés, les corrections (par exemple un facteur de correction de viscosité μ / μ paroi ) doivent être prises en compte, par exemple, comme le recommandent Sieder et Tate .
Calcul du nombre de Nusselt à l’aide de l’équation de Dittus-Boelter
Pour un écoulement turbulent pleinement développé (hydrodynamiquement et thermiquement) dans un tube circulaire lisse, le nombre de Nusselt local peut être obtenu à partir de l’ équation bien connue de Dittus ?? Boelter .
Pour calculer le nombre de Nusselt , nous devons savoir:
- le nombre de Reynolds , qui est Re Dh = 575600
- le nombre de Prandtl , qui est Pr = 0,89
Le nombre de Nusselt pour la convection forcée à l’intérieur du canal de carburant est alors égal à:
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
