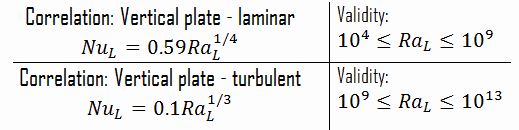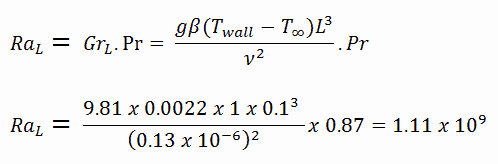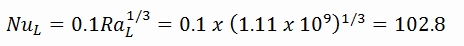Facebook Instagram Youtube Twitter

What is Laminar and Turbulent Natural Convection – Definition

by
Laminar and Turbulent Natural Convection. The microscopic nature of flow and natural convection correlations are distinctly different in the laminar and turbulent regions. Thermal Engineering

Laminar and Turbulent Natural Convection

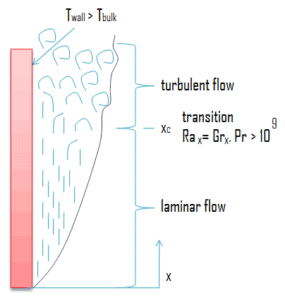Rayleigh Number and Grashof NumberIt is important to note that natural convection boundary layers are not restricted to laminar flow. As with forced convection, hydrodynamic instabilities may arise. That is, disturbances in the flow may be amplified, leading to transition from laminar to turbulent flow. For a vertical flat plate, the flow turns turbulent for value of:

Rax = Grx . Pr > 109

As in forced convection the microscopic nature of flow and convection correlations are distinctly different in the laminar and turbulent regions.

Natural Convection – Correlations

As was written, most heat transfer correlations in natural convection are based on experimental measurements and engineers often use proper characteristic numbers to describe natural convection heat transfer. The characteristic number that describes convective heat transfer (i.e. the heat transfer coefficient) is the Nusselt number, which is defined as the ratio of the thermal energy convected to the fluid to the thermal energy conducted within the fluid. The Nusselt number represents the enhancement of heat transfer through a fluid layer as a result of convection relative to conduction across the same fluid layer. But in case of free convection, heat transfer correlations (for the Nusselt number) are usually expressed in terms of the Rayleigh number.

The Rayleigh number is used to express heat transfer in natural convection. The magnitude of the Rayleigh number is a good indication as to whether the natural convection boundary layer is laminar or turbulent. The simple empirical correlations for the average Nusselt number, Nu, in natural convection are of the form:

Nux = C. Raxn

The values of the constants C and n depend on the geometry of the surface and the flow regime, which is characterized by the range of the Rayleigh number. The value of n is usually n = 1/4 for laminar flow and n = 1/3 for turbulent flow.

For example:

natural convection - heat transfer correlations

See also: Nusselt Number
See also: Rayleigh Number

Example: Natural Convection – Flat Plate

A 10cm high vertical plate is maintained at 261°C in 260°C compressed water (16MPa). Determine the Nusselt number using the simple correlation for a vertical flat plate.

example - free convection - equation

To calculate the Rayleigh number, we have to know:

  • the coefficient of thermal expansion, which is: β = 0.0022
  • the Prandtl number (for 260°C), which is: Pr = 0.87
  • the kinematic viscosity (for 260°C), which is ν = 0.13 x 10-6 (note that, this value is significantly lower than that for 20°C)

The resulting Rayleigh number is:

example - natural convection - flow regime

The resulting Nusselt number, which represents the enhancement of heat transfer through a fluid layer as a result of convection relative to conduction across the same fluid layer is:

example - natural convection - solution

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Natural Convection

We hope, this article, Laminar and Turbulent Natural Convection, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts