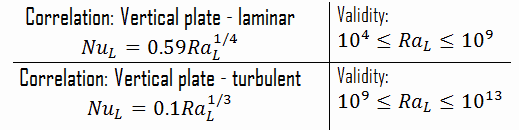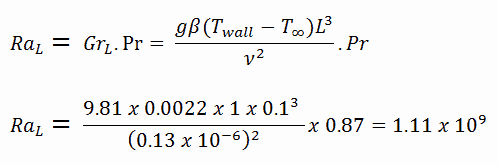Convection naturelle laminaire et turbulente
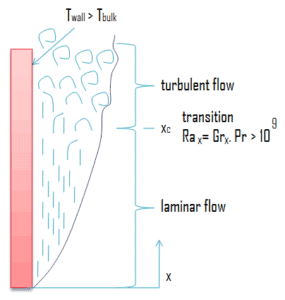
Il est important de noter que les couches limites de convection naturelle ne se limitent pas à un écoulement laminaire . Comme avec la convection forcée, des instabilités hydrodynamiques peuvent survenir. C’est-à-dire que les perturbations dans l’écoulement peuvent être amplifiées, conduisant à la transition d’un écoulement laminaire à un écoulement turbulent. Pour une plaque plate verticale, le flux devient turbulent pour une valeur de:
Ra x = Gr x . Pr> 10 9
Comme dans la convection forcée, la nature microscopique des corrélations d’écoulement et de convection est nettement différente dans les régions laminaire et turbulente .
Convection naturelle – Corrélations
Comme il a été écrit, la plupart des corrélations de transfert de chaleur en convection naturelle reposent sur des mesures expérimentales et les ingénieurs utilisent souvent des nombres de caractéristiques appropriés pour décrire le transfert de chaleur par convection naturelle. Le nombre caractéristique qui décrit le transfert de chaleur par convection (c.-à-d. Le coefficient de transfert de chaleur ) est le nombre de Nusselt , défini comme le rapport entre l’ énergie thermique convectée dans le fluide et l’ énergie thermique conduite dans le fluide. Le nombre de Nusselt représente l’amélioration du transfert de chaleur à travers une couche de fluide résultant de la convection par rapport à la conductionà travers la même couche de fluide. Mais en cas de convection libre, les corrélations de transfert de chaleur (pour le nombre de Nusselt) sont généralement exprimées en nombre de Rayleigh .
Le nombre de Rayleigh est utilisé pour exprimer le transfert de chaleur en convection naturelle. La magnitude du nombre de Rayleigh indique bien si la couche limite de convection naturelle est laminaire ou turbulente. Les corrélations empiriques simples pour le nombre moyen de Nusselt, Nu, en convection naturelle sont de la forme:
Nu x = C. Ra x n
Les valeurs des constantes C et n dépendent de la géométrie de la surface et du régime d’écoulement , qui est caractérisé par la plage du nombre de Rayleigh . La valeur de n est généralement n = 1/4 pour un écoulement laminaire et n = 1/3 pour un écoulement turbulent .
Par exemple:
Voir aussi: Nusselt Number
Voir aussi: Rayleigh Number
Exemple: Convection naturelle – Assiette plate
Une plaque verticale de 10 cm de haut est maintenue à 261 ° C dans 260 ° C d’eau comprimée (16 MPa). Déterminer le nombre de Nusselt en utilisant la corrélation simple pour une plaque plate verticale.
Pour calculer le nombre de Rayleigh, nous devons savoir:
- le coefficient de dilatation thermique, qui est: β = 0,0022
- le nombre de Prandtl (pour 260 ° C), qui est: Pr = 0,87
- la viscosité cinématique (pour 260 ° C), qui est ν = 0,13 x 10 -6 (notez que cette valeur est nettement inférieure à celle de 20 ° C)
Le nombre de Rayleigh résultant est:
Le nombre de Nusselt résultant, qui représente l’amélioration du transfert de chaleur à travers une couche de fluide en raison de la convection relative à la conduction à travers la même couche de fluide est:
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
