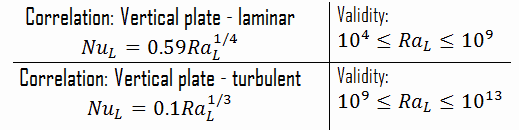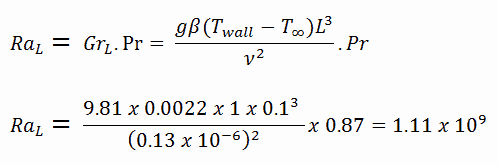Natürliche Konvektion – Freie Konvektion
 Im Allgemeinen ist Konvektion entweder der Stoffübergang oder der Wärmeübergang aufgrund der Massenbewegung von Molekülen in Flüssigkeiten wie Gasen und Flüssigkeiten. Obwohl Flüssigkeiten und Gase im Allgemeinen keine sehr guten Wärmeleiter sind, können sie Wärme durch Konvektion recht schnell übertragen. Die Konvektion erfolgt durch Advektion, Diffusion oder beides. In den vorangegangenen Kapiteln haben wir die Konvektionsübertragung in Flüssigkeitsströmen betrachtet, die von einer äußeren Zwangsbedingung herrühren – erzwungene Konvektion. In diesem Kapitel betrachten wir die natürliche Konvektion , bei der jede Flüssigkeitsbewegung auf natürliche Weise, beispielsweise durch Auftrieb, erfolgt .
Im Allgemeinen ist Konvektion entweder der Stoffübergang oder der Wärmeübergang aufgrund der Massenbewegung von Molekülen in Flüssigkeiten wie Gasen und Flüssigkeiten. Obwohl Flüssigkeiten und Gase im Allgemeinen keine sehr guten Wärmeleiter sind, können sie Wärme durch Konvektion recht schnell übertragen. Die Konvektion erfolgt durch Advektion, Diffusion oder beides. In den vorangegangenen Kapiteln haben wir die Konvektionsübertragung in Flüssigkeitsströmen betrachtet, die von einer äußeren Zwangsbedingung herrühren – erzwungene Konvektion. In diesem Kapitel betrachten wir die natürliche Konvektion , bei der jede Flüssigkeitsbewegung auf natürliche Weise, beispielsweise durch Auftrieb, erfolgt .
Definition der natürlichen Konvektion
Natürliche Konvektion , auch als freie Konvektion bezeichnet, ist ein Mechanismus oder eine Art von Stoff- und Wärmetransport , bei dem die Flüssigkeitsbewegung nur durch Dichteunterschiede in der Flüssigkeit erzeugt wird, die aufgrund von Temperaturgradienten auftreten, nicht durch eine externe Quelle (wie eine Pumpe, Lüfter, Absaugvorrichtung usw.).
Bei der natürlichen Konvektion nimmt die eine Wärmequelle umgebende Flüssigkeit Wärme auf und wird durch Wärmeausdehnung weniger dicht und steigt an. Die Wärmeausdehnung des Fluids spielt eine entscheidende Rolle. Mit anderen Worten fallen schwerere (dichtere) Komponenten, während leichtere (weniger dichte) Komponenten ansteigen, was zu einer Bewegung der Flüssigkeitsmenge führt. Natürliche Konvektion kann nur in einem Gravitationsfeld oder bei Vorhandensein einer anderen geeigneten Beschleunigung auftreten , wie zum Beispiel:
- Beschleunigung
- Zentrifugalkraft
- Corioliskraft
Natürliche Konvektion funktioniert im Wesentlichen nicht in der Erdumlaufbahn. Beispielsweise sind in der umlaufenden Internationalen Raumstation andere Wärmeübertragungsmechanismen erforderlich, um eine Überhitzung elektronischer Komponenten zu verhindern.
Natürliche Konvektion – Wärmeübertragung
Ähnlich wie bei der erzwungenen Konvektion erfolgt auch die natürliche Konvektionswärmeübertragung sowohl durch Wärmediffusion (zufällige Bewegung von Fluidmolekülen) als auch durch Advektion , bei der Materie oder Wärme durch die Bewegung von Strömen in größerem Maßstab in der Flüssigkeit transportiert wird. An der Oberfläche erfolgt der Energiefluss auch bei Konvektion nur durch Leitung . Es liegt daran, dass es immer eine dünne stehende Flüssigkeitsfilmschicht gibtauf der Wärmeübertragungsfläche. In den nächsten Schichten treten jedoch sowohl Leitungs- als auch Diffusionsmassenbewegungen auf molekularer oder makroskopischer Ebene auf. Aufgrund der Massenbewegung ist die Energieübertragungsrate höher. Je höher die Geschwindigkeit der Massenbewegung ist, desto dünner ist die stagnierende Flüssigkeitsfilmschicht und desto höher ist die Wärmestromrate.
 Wir wissen, dass die Dichte von Gasen und Flüssigkeiten von der Temperatur abhängt und im Allgemeinen (aufgrund der Flüssigkeitsausdehnung) mit zunehmender Temperatur abnimmt.Die Größe der natürlichen Konvektionswärmeübertragung zwischen einer Oberfläche und einem Fluid hängt direkt mit der Durchflussrate des Fluids zusammen, die durch natürliche Konvektion induziert wird . Je höher die Durchflussrate ist, desto höher ist die Wärmeübertragungsrate. Die Durchflussmenge bei natürlicher Konvektion wird durch das dynamische Gleichgewicht von Auftrieb und Reibung festgelegt.
Wir wissen, dass die Dichte von Gasen und Flüssigkeiten von der Temperatur abhängt und im Allgemeinen (aufgrund der Flüssigkeitsausdehnung) mit zunehmender Temperatur abnimmt.Die Größe der natürlichen Konvektionswärmeübertragung zwischen einer Oberfläche und einem Fluid hängt direkt mit der Durchflussrate des Fluids zusammen, die durch natürliche Konvektion induziert wird . Je höher die Durchflussrate ist, desto höher ist die Wärmeübertragungsrate. Die Durchflussmenge bei natürlicher Konvektion wird durch das dynamische Gleichgewicht von Auftrieb und Reibung festgelegt.
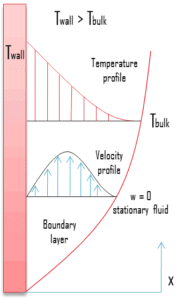
Nehmen Sie eine Platte mit der Temperatur T Wand an , die bei der Temperatur T Masse in eine ruhende Flüssigkeit eingetaucht ist , wobei ( T Wand > T Masse ). Die Flüssigkeit in der Nähe der Platte ist weniger dicht als die Flüssigkeit, die weiter entfernt wird. Auftriebskräfte induzieren daher eine natürliche Konvektionsgrenzschicht, in der die erhitzte und leichtere Flüssigkeit vertikal aufsteigt und schwerere Flüssigkeit aus dem Ruhebereich mitnimmt. Die resultierende Geschwindigkeitsverteilung unterscheidet sich von der mit erzwungene konvektionsgrenzschichten verbundenen und hängt auch von der Fluidviskosität ab. Insbesondere ist die Geschwindigkeit ist Null an der Oberfläche sowiean der Grenze aufgrund viskoser Kräfte. Es ist zu beachten, dass sich auch dann eine natürliche Konvektion entwickelt, wenn (T- Wand <T- Masse ), in diesem Fall jedoch die Flüssigkeitsbewegung nach unten erfolgt.
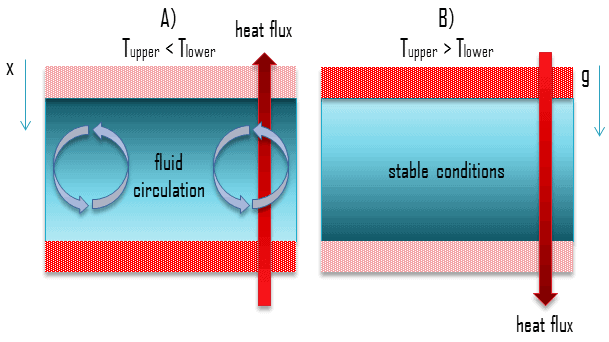
Das Vorhandensein und die Größe der natürlichen Konvektion hängen auch von der Geometrie des Problems ab. Das Vorhandensein eines Fluiddichtegradienten in einem Gravitationsfeld gewährleistet nicht die Existenz natürlicher Konvektionsströme. Dieses Problem ist in der folgenden Abbildung dargestellt, in der eine Flüssigkeit von zwei großen horizontalen Platten unterschiedlicher Temperatur (T oben ≠ T unten ) umschlossen ist .
- Im Fall A ist die Temperatur der unteren Platte höher als die Temperatur der oberen Platte. In diesem Fall nimmt die Dichte in Richtung der Gravitationskraft ab. Diese Geometrie induziert die Flüssigkeitszirkulation und die Wärmeübertragung erfolgt über die natürliche Zirkulation. Die schwerere Flüssigkeit steigt ab und wird dabei erwärmt, während die leichtere Flüssigkeit aufsteigt und sich abkühlt, wenn sie sich bewegt.
- In Fall B ist die Temperatur der unteren Platte niedriger als die Temperatur der oberen Platte. In diesem Fall nimmt die Dichte in Richtung der Gravitationskraft zu. Diese Geometrie führt zu stabilen Bedingungen, einem stabilen Temperaturgradienten und induziert keine Flüssigkeitszirkulation . Die Wärmeübertragung erfolgt ausschließlich über Wärmeleitung .
Da die natürliche Konvektion stark von der Geometrie abhängt, basieren die meisten Wärmeübertragungskorrelationen bei der natürlichen Konvektion auf experimentellen Messungen, und Ingenieure verwenden häufig geeignete Kennzahlen, um die natürliche Konvektionswärmeübertragung zu beschreiben.
Natürliche Konvektion – Korrelationen
Wie bereits geschrieben, basieren die meisten Korrelationen der Wärmeübertragung bei der natürlichen Konvektion auf experimentellen Messungen, und Ingenieure verwenden häufig geeignete Kennzahlen , um die Wärmeübertragung bei der natürlichen Konvektion zu beschreiben. Die charakteristische Zahl, die die konvektive Wärmeübertragung beschreibt (dh den Wärmeübergangskoeffizienten ), ist die Nusselt-Zahl , die als das Verhältnis der zum Fluid übertragenen Wärmeenergie zur im Fluid geleiteten Wärmeenergie definiert ist . Die Nusselt-Zahl repräsentiert die Verbesserung der Wärmeübertragung durch eine Fluidschicht infolge der Konvektion im Verhältnis zur Leitungüber die gleiche Flüssigkeitsschicht. Bei freier Konvektion werden die Wärmeübertragungskorrelationen (für die Nusselt-Zahl) normalerweise in Form der Rayleigh-Zahl ausgedrückt .
Die Rayleigh-Zahl wird verwendet, um die Wärmeübertragung in natürlicher Konvektion auszudrücken. Die Größe der Rayleigh-Zahl ist ein guter Hinweis darauf, ob die natürliche Konvektionsgrenzschicht laminar oder turbulent ist. Die einfachen empirischen Korrelationen für die durchschnittliche Nusselt-Zahl Nu in natürlicher Konvektion haben folgende Form:
Nu x = C. Ra x n
Die Werte der Konstanten C und n hängen von der Geometrie der Oberfläche und dem Strömungsregime ab , das durch den Bereich der Rayleigh-Zahl gekennzeichnet ist . Der Wert von n ist normalerweise n = 1/4 für laminare Strömung und n = 1/3 für turbulente Strömung .
Beispielsweise:
Siehe auch: Nusselt-Nummer
Siehe auch: Rayleigh-Nummer
Beispiel: Natürliche Konvektion – flache Platte
Eine 10 cm hohe vertikale Platte wird in 260 ° C Druckwasser (16 MPa) bei 261 ° C gehalten. Bestimmen Sie die Nusselt-Zahl anhand der einfachen Korrelation für eine vertikale flache Platte.
Um die Rayleigh-Zahl zu berechnen, müssen wir wissen:
- der Wärmeausdehnungskoeffizient, der ist: β = 0,0022
- die Prandtl-Zahl (für 260 ° C), die ist: Pr = 0,87
- die kinematische Viskosität (für 260 ° C), die ν = 0,13 × 10 –6 beträgt (beachten Sie, dass dieser Wert signifikant niedriger ist als der für 20 ° C)
Die resultierende Rayleigh-Zahl lautet:
Die resultierende Nusselt-Zahl, die die Verbesserung der Wärmeübertragung durch eine Fluidschicht als Ergebnis der Konvektion im Verhältnis zur Leitung durch dieselbe Fluidschicht darstellt, ist:
Kombinierte erzwungene und natürliche Konvektion
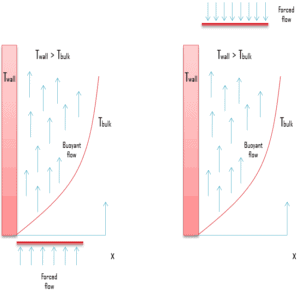 Wie geschrieben wurde, erfolgt die Konvektion durch Advektion, Diffusion oder beides. In den vorhergehenden Kapiteln haben wir die Konvektionstransfer in Flüssigkeitsströmen betrachtet, die von einer externen Zwangsbedingung herrühren – erzwungene Konvektion . In diesem Kapitel betrachten wir die natürliche Konvektion , bei der jede Flüssigkeitsbewegung durch natürliche Mittel wie Auftrieb erfolgt. Tatsächlich gibt es Strömungsregime, in denen wir beide Zwangsmechanismen berücksichtigen müssen . Wenn die Strömungsgeschwindigkeiten niedrig sind, trägt neben der erzwungenen Konvektion auch die natürliche Konvektion bei. Ob die freie Konvektion für die Wärmeübertragung von Bedeutung ist oder nicht, kann anhand der folgenden Kriterien überprüft werden:
Wie geschrieben wurde, erfolgt die Konvektion durch Advektion, Diffusion oder beides. In den vorhergehenden Kapiteln haben wir die Konvektionstransfer in Flüssigkeitsströmen betrachtet, die von einer externen Zwangsbedingung herrühren – erzwungene Konvektion . In diesem Kapitel betrachten wir die natürliche Konvektion , bei der jede Flüssigkeitsbewegung durch natürliche Mittel wie Auftrieb erfolgt. Tatsächlich gibt es Strömungsregime, in denen wir beide Zwangsmechanismen berücksichtigen müssen . Wenn die Strömungsgeschwindigkeiten niedrig sind, trägt neben der erzwungenen Konvektion auch die natürliche Konvektion bei. Ob die freie Konvektion für die Wärmeübertragung von Bedeutung ist oder nicht, kann anhand der folgenden Kriterien überprüft werden:
- Wenn Gr / Re 2 >> 1 herrscht, herrscht freie Konvektion
- Wenn Gr / Re 2 << 1 ist, herrscht erzwungene Konvektion
- Wenn Gr / Re 2 ≈ 1 ist, sollten beide berücksichtigt werden
Die Auswirkung des Auftriebs auf die Wärmeübertragung in einer erzwungenen Strömung wird stark von der Richtung der Auftriebskraft relativ zu der der Strömung beeinflusst. Natürliche Konvektion kann die Wärmeübertragung durch erzwungene Konvektion unterstützen oder beeinträchtigen , abhängig von den relativen Richtungen der durch Auftrieb induzierten und erzwungenen Konvektionsbewegungen. Drei ausgiebig untersuchte Sonderfälle entsprechen Auftriebs- und Zwangsbewegungen:
- Unterstützung des Flusses . Die Auftriebsbewegung erfolgt in die gleiche Richtung wie die erzwungene Bewegung.
- Gegenströmung . Die Auftriebsbewegung ist entgegengesetzt zur erzwungenen Bewegung.
- Querströmung . Die Auftriebsbewegung ist senkrecht zur erzwungenen Bewegung.
Es ist offensichtlich, dass der Auftrieb bei unterstützenden und quer verlaufenden Strömungen die Wärmeübertragungsrate erhöht, die mit einer reinen erzwungenen Konvektion verbunden ist. Andererseits verringert es bei entgegengesetzten Strömungen die Wärmeübertragungsrate. Bei der Bestimmung der Nusselt-Zahl unter kombinierten natürlichen und erzwungenen Konvektionsbedingungen ist es verlockend, die Beiträge der natürlichen und erzwungenen Konvektion zur Unterstützung von Strömungen zu addieren und in entgegengesetzten Strömungen zu subtrahieren:
Für die spezifische interessierende Geometrie werden die Nusselt-Zahlen Nu Forced und Nu Natural aus vorhandenen Korrelationen für die reine forcierte bzw. natürliche (freie) Konvektion bestimmt. Die beste Korrelation von Daten zu Experimenten wird häufig für den Exponenten n = 3 erhalten , kann jedoch je nach Geometrie des Problems zwischen 3 und 4 variieren.
Natürliche Zirkulation
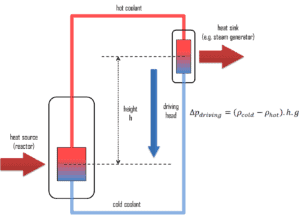
Natürliche Zirkulation ist die Zirkulation von Flüssigkeit in Rohrleitungssystemen oder offenen Becken , die auf Dichteänderungen zurückzuführen ist, die durch Temperaturunterschiede verursacht werden. Für die natürliche Zirkulation sind keine mechanischen Geräte erforderlich, um den Durchfluss aufrechtzuerhalten.
Dieses Phänomen hat eine ähnliche Natur wie die natürliche Konvektion, aber in diesem Fall ist der Wärmeübergangskoeffizient kein Untersuchungsgegenstand. In diesem Fall ist der Volumenstrom durch die Schleife Gegenstand der Untersuchung. Dieses Phänomen ist eher ein hydraulisches Problem als ein Wärmeübertragungsproblem, obwohl die natürliche Zirkulation die Wärme von der Quelle abführt und zum Kühlkörper transportiert und für die Reaktorsicherheit von höchster Bedeutung ist.
Siehe auch: Natürliche Zirkulation
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.