Was ist Pumpenkopfberechnung – Berechnung der Pumpenleistung – Definition

Pumpenkopfberechnung – Berechnung der Pumpenleistung

In diesem Beispiel werden wir sehen, wie man vorhersagt

• die Designentladung
• Wasserleistung
• der Pumpenkopf

einer Kreiselpumpe . Diese Leistungsdaten werden aus der Euler-Turbomaschinengleichung abgeleitet:

    Wellendrehmoment : T _Welle = ρQ (r ₂ V _t2 – r ₁ V _t1 )

Wasserleistung: P _w         = ω. T _Welle        = ρQ (u ₂ V _t2 – u ₁ V _t1 )

Pumpenkopf : H = P _w / ρgQ = (u ₂ V _t2 – u ₁ V _t1 ) / g

Gegeben sind folgende Daten für eine Kreiselwasserpumpe:

• Durchmesser des Laufrads am Einlass und Auslass
  • r ₁ = 10 cm
  • r ₂ = 20 cm
• Geschwindigkeit = 1500 U / min (Umdrehungen pro Minute)
• der Schaufelwinkel am Einlass β ₁ = 30 °
• der Schaufelwinkel am Auslass β ₂ = 20 °
• Angenommen, die Schaufelbreiten am Einlass und Auslass betragen: b ₁ = b ₂ = 4 cm .

Lösung:

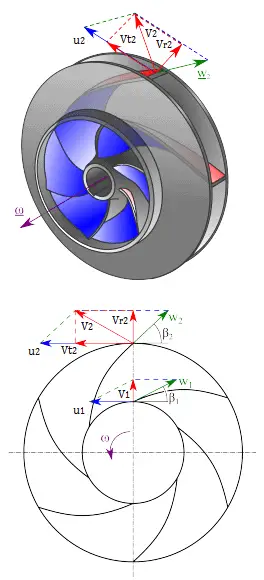
Zuerst müssen wir die Radialgeschwindigkeit der Strömung am Auslass berechnen . Aus dem Geschwindigkeitsdiagramm ist die Radialgeschwindigkeit gleich (wir nehmen an, dass die Strömung genau normal zum Laufrad eintritt, sodass die tangentiale Geschwindigkeitskomponente Null ist):

V _r1 = u ₁ tan 30 ° = & ohgr; r ₁ tan 30 ° = 2 & pgr; x (1500/60) x 0,1 x tan 30 ° = 9,1 m / s

Die radiale Komponente der Strömungsgeschwindigkeit bestimmt, wie stark der Volumenstrom in das Laufrad eintritt . Wenn wir also V _r1 am Einlass kennen, können wir den Ausstoß dieser Pumpe gemäß der folgenden Gleichung bestimmen . Hier bedeutet b ₁ die Schaufelbreite des Laufrads am Einlass.

Q = 2π.r ₁ .b ₁ .V _r1 = 2π x 0,1 x 0,04 x 9,1 = 0,229 m ³ / s

Um die erforderliche Wasserleistung (P _w ) zu berechnen , müssen wir die Tangentialströmungsgeschwindigkeit V _t2 des Auslasses bestimmen , da angenommen wurde, dass die Tangentialgeschwindigkeit V _t1 des Einlasses gleich Null ist.

Die radiale Auslassströmungsgeschwindigkeit ergibt sich aus der Erhaltung von Q :

Q = 2π.r ₂ .b ₂ .V _r2  ⇒ V _r2 = Q / 2π.r ₂ .b ₂ = 0,229 / (2π x 0,2 x 0,04) =  4,56 m / s

Aus der Figur ( Geschwindigkeitsdreieck ) kann der Auslassschaufelwinkel β ₂ leicht wie folgt dargestellt werden.

cot β ₂ = (u ₂ – V _t2 ) / V _r2

und daher ist die tangentiale Strömungsgeschwindigkeit V _t2 am Auslass :

V _t2 = u ₂ – V _r2 . 20 ° cot = ω r ₂ – V _r2 . Kinderbett 20 ° = 2 & pgr; x 1500/60 x 0,2 – 4,56 x 2,75 = 31,4 – 12,5 = 18,9 m / s.

Die erforderliche Wasserleistung beträgt dann:

P _w  = ρ Q U ₂ V _t2 = 1000 [kg / m ³ ] 0,229 x [m ³ / s] 31,4 x [m / s] 18,9 x [m / s] = 135900 W = 135,6 kW

und der Pumpenkopf ist:

H ≤ P _w / (ρ g Q) = 135900 / (1000 × 9,81 × 0,229) = 60,5 m