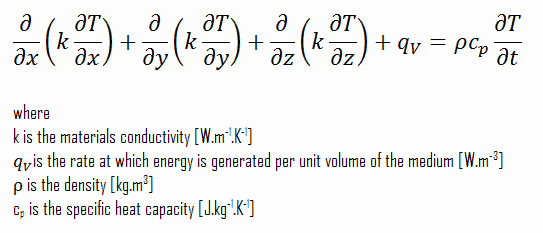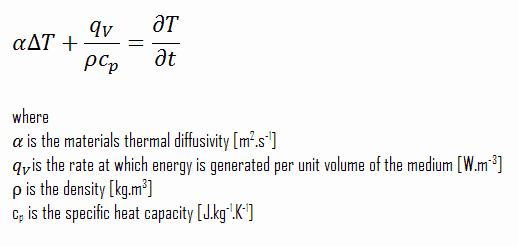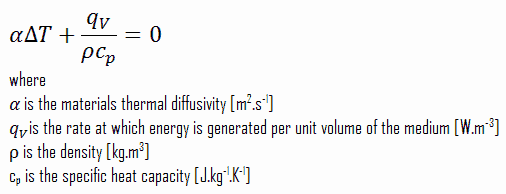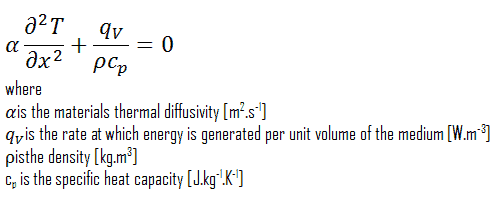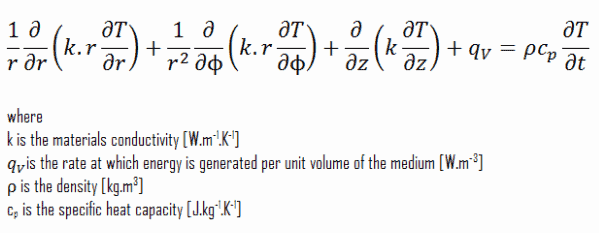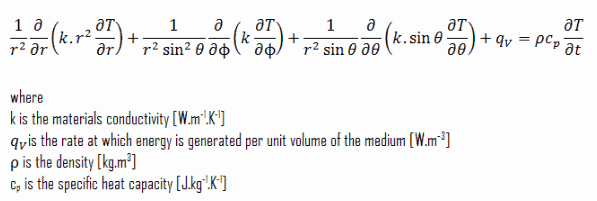Wärmegleichung – Wärmeleitungsgleichung
 In früheren Abschnitten haben wir uns speziell mit eindimensionaler stationärer Wärmeübertragung befasst, die durch das Fourier-Gesetz der Wärmeleitung charakterisiert werden kann . Ihre Anwendbarkeit ist jedoch sehr begrenzt. Dieses Gesetz geht von einer stationären Wärmeübertragung durch einen planaren Körper aus (beachte, dass das Fourier-Gesetz auch für zylindrische und sphärische Koordinaten abgeleitet werden kann), ohne Wärmequellen . Es ist einfach die Geschwindigkeitsgleichung in diesem Wärmeübertragungsmodus, bei der der Temperaturgradient bekannt ist.
In früheren Abschnitten haben wir uns speziell mit eindimensionaler stationärer Wärmeübertragung befasst, die durch das Fourier-Gesetz der Wärmeleitung charakterisiert werden kann . Ihre Anwendbarkeit ist jedoch sehr begrenzt. Dieses Gesetz geht von einer stationären Wärmeübertragung durch einen planaren Körper aus (beachte, dass das Fourier-Gesetz auch für zylindrische und sphärische Koordinaten abgeleitet werden kann), ohne Wärmequellen . Es ist einfach die Geschwindigkeitsgleichung in diesem Wärmeübertragungsmodus, bei der der Temperaturgradient bekannt ist.
Ein Hauptproblem bei den meisten Leitungsanalysen besteht jedoch darin, das Temperaturfeld in einem Medium zu bestimmen, das sich aus den Bedingungen ergibt, die an seinen Grenzen herrschen. In der Technik müssen wir Wärmeübertragungsprobleme lösen, die unterschiedliche Geometrien und Bedingungen betreffen, z. B. ein zylindrisches Kernbrennelement, an dem eine interne Wärmequelle oder die Wand eines kugelförmigen Containments beteiligt ist. Diese Probleme sind komplexer als die planaren Analysen, die wir in den vorherigen Abschnitten durchgeführt haben. Daher werden diese Probleme Gegenstand dieses Abschnitts sein, in dem die Wärmeleitungsgleichung eingeführt und gelöst wird.
Allgemeine Wärmeleitungsgleichung
Die Wärmeleitungsgleichung ist eine partielle Differentialgleichung, die die Verteilung der Wärme (oder des Temperaturfeldes ) in einem bestimmten Körper über die Zeit beschreibt. Detaillierte Kenntnisse des Temperaturfeldes sind für die Wärmeleitung durch Materialien sehr wichtig. Sobald diese Temperaturverteilung bekannt ist, kann der Wärmeleitungsfluss an jedem Punkt im Material oder auf seiner Oberfläche nach dem Fourier-Gesetz berechnet werden .
Die Wärmegleichung leitet sich aus dem Fourier-Gesetz und der Energieerhaltung ab . Das Fourier-Gesetz besagt, dass die zeitliche Wärmeübertragungsrate durch ein Material proportional zum negativen Temperaturgradienten und zu der Fläche im rechten Winkel zu dem Gradienten ist, durch den die Wärme fließt.
Eine Änderung der inneren Energie pro Volumeneinheit im Material ΔQ ist proportional zur Änderung der Temperatur Δu. Das ist:
∆Q = ρ.c p .∆T
Generelle Form
Unter Verwendung dieser beiden Gleichungen können wir die allgemeine Wärmeleitungsgleichung ableiten:
Diese Gleichung wird auch als Fourier-Biot-Gleichung bezeichnet und bietet das grundlegende Werkzeug für die Wärmeleitungsanalyse. Aus seiner Lösung können wir das Temperaturfeld als Funktion der Zeit erhalten.
In Worten heißt es in der Wärmeleitungsgleichung :
Zu jedem Zeitpunkt im Medium muss die Nettorate der Energieübertragung durch Leitung in ein Volumeneinheit plus die Volumenrate der Wärmeenergieerzeugung gleich der Änderungsrate der im Volumen gespeicherten Wärmeenergie sein.
Konstante Wärmeleitfähigkeit und stationäre Wärmeübertragung – Poissonsche GleichungZusätzliche Vereinfachungen der allgemeinen Form der Wärmegleichung sind häufig möglich. Beispielsweise kann sich unter stationären Bedingungen die Menge des Energiespeichers nicht ändern (∂T / ∂t = 0).
Eindimensionale Wärmegleichung
Eine der schlagkräftigsten Annahmen ist, dass der Sonderfall der eindimensionalen Wärmeübertragung in x-Richtung. In diesem Fall fallen die Ableitungen in Bezug auf y und z aus und die obigen Gleichungen reduzieren sich auf (kartesische Koordinaten):
Wärmeleitung in zylindrischen und sphärischen Koordinaten
In der Technik gibt es viele Probleme, die mit kartesischen Koordinaten nicht gelöst werden können. Zylindrische und kugelförmige Systeme sind in der thermischen und insbesondere in der Energietechnik sehr verbreitet. Die Wärmegleichung kann auch in Zylinder- und Kugelkoordinaten ausgedrückt werden. Die allgemeine Wärmeleitungsgleichung in Zylinderkoordinaten kann aus einer Energiebilanz eines Volumenelements in Zylinderkoordinaten und unter Verwendung des Laplace-Operators Δ in zylindrischer und sphärischer Form erhalten werden .
Zylinderkoordinaten:
Sphärische Koordinaten:
Um analytische Lösungen für diese Differentialgleichungen zu erhalten, müssen die Lösungstechniken partieller Differentialgleichungen bekannt sein, was den Rahmen dieses Textes sprengt. Andererseits gibt es viele Vereinfachungen und Annahmen, die auf diese Gleichungen angewendet werden können und zu sehr wichtigen Ergebnissen führen. Im nächsten Abschnitt beschränken wir uns auf eindimensionale stationäre Fälle mit konstanter Wärmeleitfähigkeit, da sie zu gewöhnlichen Differentialgleichungen führen.
Rand- und Anfangsbedingungen
Wie bei einer anderen Differentialgleichung ist die Lösung durch Rand- und Anfangsbedingungen gegeben . In Bezug auf die Randbedingungen gibt es mehrere gemeinsame Möglichkeiten, die einfach in mathematischer Form ausgedrückt werden.
Da die Wärmeleitungsgleichung zweiter Ordnung ist in den räumlichen Koordinaten, um ein Wärmeübertragungs Problem vollständig zu beschreiben, zwei Randbedingungen muß gegeben werden für jede Richtung des Koordinatensystems , entlang derer die Wärmeübertragung signifikant. Daher müssen wir vier Randbedingungen für zweidimensionale Probleme und sechs Randbedingungen für dreidimensionale Probleme angeben.
Im folgenden Abschnitt werden vier Arten von Randbedingungen zusammengefasst, die bei der Wärmeübertragung häufig auftreten:
Leitung mit Wärmeerzeugung
 Im vorhergehenden Abschnitt betrachteten wir Wärmeleitungsprobleme ohne interne Wärmequellen . Für diese Probleme wurde die Temperaturverteilung in einem Medium ausschließlich durch Bedingungen an den Grenzen des Mediums bestimmt. In der Technik können wir jedoch häufig auf ein Problem stoßen, bei dem interne Wärmequellen von Bedeutung sind und die Temperaturverteilung zusammen mit den Randbedingungen bestimmen.
Im vorhergehenden Abschnitt betrachteten wir Wärmeleitungsprobleme ohne interne Wärmequellen . Für diese Probleme wurde die Temperaturverteilung in einem Medium ausschließlich durch Bedingungen an den Grenzen des Mediums bestimmt. In der Technik können wir jedoch häufig auf ein Problem stoßen, bei dem interne Wärmequellen von Bedeutung sind und die Temperaturverteilung zusammen mit den Randbedingungen bestimmen.
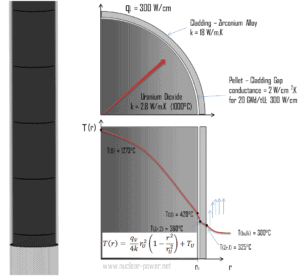
In der Nukleartechnik sind diese Probleme von höchster Bedeutung, da der größte Teil der im Kernbrennstoff erzeugten Wärme in den Brennstoffpellets freigesetzt wird und die Temperaturverteilung hauptsächlich durch die Wärmeerzeugungsverteilung bestimmt wird. Es ist zu beachten, dass, wie aus der Beschreibung der einzelnen Komponenten der Gesamtenergie, die während der Spaltreaktion freigesetzt wird, ersichtlich ist, eine erhebliche Energiemenge außerhalb des Kernbrennstoffs (außerhalb der Brennstäbe) erzeugt wird. Insbesondere die kinetische Energie von sofortigen Neutronen wird weitgehend im Kühlmittel ( Moderator ) erzeugt . Dieses Phänomen muss in die nuklearen Berechnungen einbezogen werden.
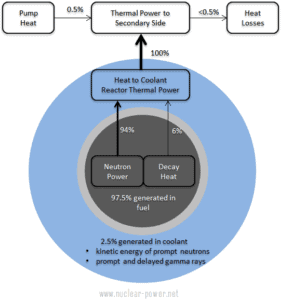
Für LWR wird allgemein angenommen, dass etwa 2,5% der Gesamtenergie im Moderator zurückgewonnen werden . Dieser Energieanteil hängt von den Materialien, ihrer Anordnung innerhalb des Reaktors und damit vom Reaktortyp ab.
Beachten Sie, dass die Wärmeerzeugung ein volumetrisches Phänomen ist. Das heißt, es tritt im gesamten Körper eines Mediums auf. Daher wird die Wärmeerzeugungsrate in einem Medium üblicherweise pro Volumeneinheit angegeben und mit g V [W / m 3 ] bezeichnet .
Die Temperaturverteilung und dementsprechend der Wärmefluss wird hauptsächlich bestimmt durch:
- Geometrie und Randbedingungen . Unterschiedliche Geometrie führt zu völlig unterschiedlichen Temperaturfeldern.
- Wärmeerzeugungsrate . Der Temperaturabfall durch den Körper nimmt mit zunehmender Wärmeerzeugung zu.
- Wärmeleitfähigkeit des Mediums . Eine höhere Wärmeleitfähigkeit führt zu einem geringeren Temperaturabfall.
Lösung der Wärmegleichung
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.