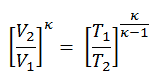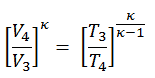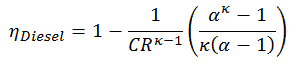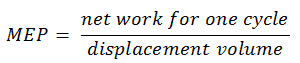¿Qué es el ciclo diesel? Problema con la solución: definición

Ciclo diésel: problema con la solución

Ciclo diésel: problema con la solución

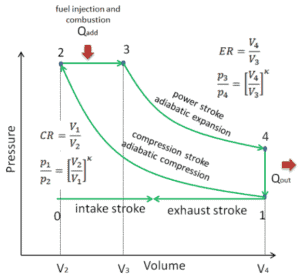
Supongamos el ciclo Diesel, que es uno de los ciclos termodinámicos más comunes que se pueden encontrar en los motores de automóviles . Uno de los parámetros clave de tales motores es el cambio en los volúmenes entre el punto muerto superior (TDC) y el punto muerto inferior (BDC). La relación de estos volúmenes ( V ₁ / V ₂ ) se conoce como la relación de compresión . También la relación de corte V ₃ / V ₂ , que es la relación de volúmenes al final y al inicio de la fase de combustión.

En este ejemplo, supongamos el ciclo Diesel con una relación de compresión de CR = 20: 1 y una relación de corte α = 2. El aire está a 100 kPa = 1 bar, 20 ° C (293 K) y el volumen de la cámara es 500 cm³ antes de la carrera de compresión.

• Capacidad calorífica específica a presión constante del aire a presión atmosférica y temperatura ambiente: c _p = 1,01 kJ / kgK.
• Capacidad calorífica específica a volumen constante de aire a presión atmosférica y temperatura ambiente: c _v = 0.718 kJ / kgK.
• κ = c _p / c _v = 1.4

Calcular:

1. la masa de aire de admisión
2. la temperatura T ₂
3. la presión p ₂
4. la temperatura T ₃
5. la cantidad de calor agregado al quemar la mezcla de combustible y aire
6. la eficiencia térmica de este ciclo
7. el eurodiputado

Solución:

1)

Al comienzo de los cálculos tenemos que determinar la cantidad de gas en el cilindro antes de la carrera de compresión. Usando la ley de los gases ideales, podemos encontrar la masa:

pV = mR _específico T

dónde:

• p es la presión absoluta del gas
• m es la masa de sustancia
• T es la temperatura absoluta
• V es el volumen
• R _específica es la constante de gas específica, igual a la constante de gas universal dividida por la masa molar (M) del gas o mezcla. Para aire seco R _específico = 287.1 J.kg ^-1 .K ^-1 .

Por lo tanto

m = p ₁ V ₁ / R _específico T ₁ = (100000 × 500 × ^10-6 ) / (287.1 × 293) = 5.95 × 10 ^-4 kg

2)

En este problema se conocen todos los volúmenes:

• V ₁ = V ₄ = V _máx = 500 × 10 ^-6 m ³ (0.5l)
• V ₂ = V _min = V _max / CR = 25 × 10 ^-6 m ³

Tenga en cuenta que (V _max – V _min ) x número de cilindros = desplazamiento total del motor

Dado que el proceso es adiabático, podemos usar la siguiente relación p, V, T para procesos adiabáticos:

así

T ₂ = T ₁ . CR ^{κ – 1} = 293. 20 ^0.4 = 971 K

3)

Nuevamente, podemos usar la ley de los gases ideales para encontrar la presión al final de la carrera de compresión como:

p ₂ = mR _específico T ₂ / V ₂ = 5.95 × 10 ^-4 x 287.1 x 971/25 × 10 ^-6 = 6635000 Pa = 66.35 bar

4)

Como el proceso 2 → 3 ocurre a presión constante, la ecuación de estado de gas ideal da

T ₃ = (V ₃ / V ₂ ) x T ₂ = 1942 K

Para calcular la cantidad de calor agregado al quemar la mezcla de combustible y aire, _agregue Q , tenemos que usar la primera ley de la termodinámica para el proceso isobárico, que establece:

Q _add = mc _p (T ₃ – T ₂ ) = 5.95 × 10 ^-4 x 1010 x 971 = 583.5 J

5)

Eficiencia térmica para este ciclo Diesel:

Como se dedujo en la sección anterior, la eficiencia térmica del ciclo Diesel es una función de la relación de compresión, la relación de corte y κ:

dónde

• η _Diesel es la máxima eficiencia térmica de un ciclo Diesel
• α es la relación de corte V ₃ / V ₂ (es decir, la relación de volúmenes al final y al inicio de la fase de combustión)
• CR es la relación de compresión
• κ = c _p / c _v = 1.4

Para este ejemplo:

η _Diesel = 0.6467 = 64.7%

6)

El MEP se definió como:

En esta ecuación, el volumen de desplazamiento es igual a V _max – V _min . El trabajo neto para un ciclo se puede calcular utilizando el calor agregado y la eficiencia térmica:

W _net = Q _add . η _Otto = 583.5 x 0.6467 = 377.3 J

MEP = 377.3 / ( 500 × ^10-6 – 25 × 10 ^-6 ) = 794.3 kPa = 7.943 bar