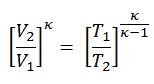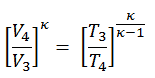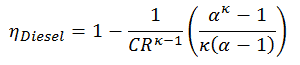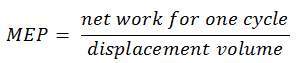What is Diesel Cycle – Problem with Solution – Definition

Diesel Cycle – Problem with Solution

Diesel Cycle – Problem with Solution

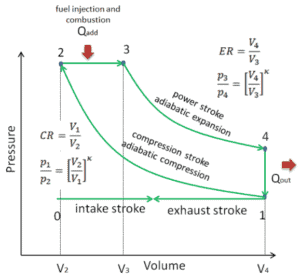
Let assume the Diesel cycle, which is the one of most common thermodynamic cycles that can be found in automobile engines. One of key parameters of such engines is the change in volumes between top dead center (TDC) to bottom dead center (BDC). The ratio of these volumes (V₁ / V₂) is known as the compression ratio. Also the cut-off ratio V₃/V₂, which is the ratio of volumes at the end and start of the combustion phase.

In this example let assume the Diesel cycle with compression ratio of CR = 20 : 1 and cut-off ratio α = 2. The air is at 100 kPa = 1 bar, 20 °C (293 K), and the volume of the chamber is 500 cm³ prior to the compression stroke.

• Specific heat capacity at constant pressure of air at atmospheric pressure and room temperature: c_p = 1.01 kJ/kgK.
• Specific heat capacity at constant volume of air at atmospheric pressure and room temperature: c_v = 0.718 kJ/kgK.
• κ = c_p/c_v = 1.4

Calculate:

1. the mass of intake air
2. the temperature T₂
3. the pressure p₂
4. the temperature T₃
5. the amount of heat added by burning of fuel-air mixture
6. the thermal efficiency of this cycle
7. the MEP

Solution:

1)

At the beginning of calculations we have to determine the amount of gas in the cylinder before the compression stroke. Using the ideal gas law, we can find the mass:

pV = mR_specificT

where:

• p is the absolute pressure of the gas
• m is the mass of substance
• T is the absolute temperature
• V is the volume
• R_specific is the specific gas constant, equal to the universal gas constant divided by the molar mass (M) of the gas or mixture. For dry air R_specific = 287.1 J.kg^-1.K^-1.

Therefore

m = p₁V₁/R_specificT₁ = (100000 × 500×10^-6 )/(287.1 × 293) = 5.95×10^-4 kg

2)

In this problem all volumes are known:

• V₁ = V₄ = V_max = 500×10^-6 m³ (0.5l)
• V₂ = V_min = V_max / CR = 25 ×10^-6 m³

Note that (V_max – V_min) x number of cylinders = total engine displacement

Since the process is adiabatic, we can use the following p, V, T relation for adiabatic processes:

thus

T₂ = T₁ . CR^{κ – 1} = 293 . 20^0.4 = 971 K

3)

Again, we can use the ideal gas law to find the pressure at the end of the compression stroke as:

p₂ = mR_specificT₂ / V₂ = 5.95×10^-4 x 287.1 x 971 / 25 ×10^-6 = 6635000 Pa = 66.35 bar

4)

Since process 2 → 3 occurs at constant pressure, the ideal gas equation of state gives

T₃ = (V₃/V₂) x T₂ = 1942 K

To calculate the amount of heat added by burning of fuel-air mixture, Q_add, we have to use the first law of thermodynamics for isobaric process, which states:

Q_add = mc_p (T₃ – T₂) = 5.95×10^-4 x 1010 x 971 = 583.5 J

5)

Thermal efficiency for this Diesel cycle:

As was derived in the previous section, the thermal efficiency of Diesel cycle is a function of the compression ratio, the cut-off ratio and κ:

where

• η_Diesel is the maximum thermal efficiency of a Diesel cycle
• α is the cut-off ration V₃/V₂ (i.e. the ratio of volumes at the end and start of the combustion phase)
• CR is the compression ratio
• κ = c_p/c_v = 1.4

For this example:

η_Diesel = 0.6467 = 64.7%

6)

The MEP was defined as:

It this equation the displacement volume is equal to V_max – V_min. The net work for one cycle can be calculated using the heat added and the thermal efficiency:

W_net = Q_add . η_Otto = 583.5 x 0.6467 = 377.3 J

MEP = 377.3 / (500×10^-6 – 25 ×10^-6) = 794.3 kPa = 7.943 bar

See also:

Diesel Cycle