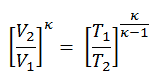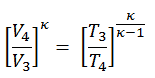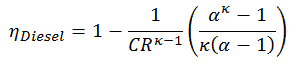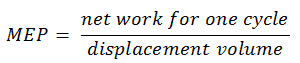Ciclo Diesel – Problema com a Solução
Ciclo Diesel – Problema com a Solução
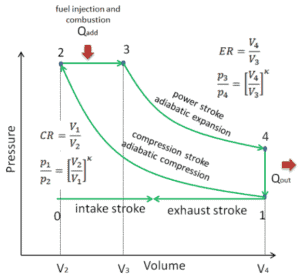
Vamos assumir o ciclo Diesel, que é um dos ciclos termodinâmicos mais comuns encontrados em motores de automóveis . Um dos principais parâmetros desses motores é a mudança de volumes entre o ponto morto superior (TDC) e o ponto morto inferior (BDC). A proporção desses volumes ( V 1 / V 2 ) é conhecida como taxa de compressão . Também a relação de corte V 3 / V 2 , que é a relação dos volumes no final e no início da fase de combustão.
Neste exemplo, vamos assumir o ciclo Diesel com taxa de compressão de CR = 20: 1 e taxa de corte α = 2. O ar está a 100 kPa = 1 bar, 20 ° C (293 K) e o volume da câmara é de 500 cm³ antes do curso de compressão.
- Capacidade térmica específica a pressão constante do ar à pressão atmosférica e à temperatura ambiente: c p = 1,01 kJ / kgK.
- Capacidade térmica específica a um volume constante de ar à pressão atmosférica e à temperatura ambiente: c v = 0,718 kJ / kgK.
- κ = c p / c v = 1,4
Calcular:
- a massa de entrada de ar
- a temperatura T 2
- a pressão p 2
- a temperatura T 3
- a quantidade de calor adicionada pela queima da mistura combustível-ar
- a eficiência térmica deste ciclo
- o deputado
Solução:
1)
No início dos cálculos, temos que determinar a quantidade de gás no cilindro antes do curso de compressão. Usando a lei do gás ideal, podemos encontrar a massa:
pV = mR específico T
Onde:
- p é a pressão absoluta do gás
- m é a massa da substância
- T é a temperatura absoluta
- V é o volume
- R específico é a constante de gás específica, igual à constante de gás universal dividida pela massa molar (M) do gás ou mistura. Para ar seco R específico = 287,1 J.kg -1 .K -1 .
Portanto
m = p 1 V 1 / R específico T 1 = (100000 × 500 × 10 -6 ) / (287,1 × 293) = 5,95 × 10 -4 kg
2)
Nesse problema, todos os volumes são conhecidos:
- V 1 = V 4 = V max = 500 × 10 -6 m 3 (0,5l)
- V 2 = V min = V máx / CR = 25 × 10 -6 m 3
Observe que (V max – V min ) x número de cilindros = cilindrada total do motor
Como o processo é adiabático, podemos usar a seguinte relação p, V, T para processos adiabáticos:
portanto
T 2 = T 1 . CR k – 1 = 293. 20 0,4 = 971 K
3)
Novamente, podemos usar a lei do gás ideal para encontrar a pressão no final do curso de compressão como:
P 2 = mR específico T 2 / V 2 = 5,95 x 10 -4 x 287,1 x 971/25 x 10 -6 = 6.635.000 Pa = 66,35 barra
4)
Como o processo 2 → 3 ocorre a pressão constante, a equação ideal de estado do gás fornece
T 3 = (V 3 / V 2 ) x T 2 = 1942 K
Para calcular a quantidade de calor adicionada pela queima da mistura combustível-ar, adicione Q , precisamos usar a primeira lei da termodinâmica para o processo isobárico, que afirma:
Q add = mc p (T 3 – T 2 ) = 5,95 x 10 -4 x 1010 x 971 = 583,5 J
5)
Eficiência térmica para este ciclo Diesel:
Como foi derivado na seção anterior, a eficiência térmica do ciclo Diesel é uma função da taxa de compressão, da taxa de corte e κ:
Onde
- η Diesel é a eficiência térmica máxima de um ciclo Diesel
- α é a razão de corte V 3 / V 2 (ou seja, a razão de volumes no final e no início da fase de combustão)
- CR é a taxa de compressão
- κ = c p / c v = 1,4
Para este exemplo:
η Diesel = 0,6467 = 64,7%
6)
O MEP foi definido como:
Nesta equação, o volume de deslocamento é igual a V max – V min . O trabalho líquido para um ciclo pode ser calculado usando o calor adicionado e a eficiência térmica:
W net = Q add . η Otto = 583,5 x 0,6467 = 377,3 J
MEP = 377,3 / ( 500 × 10 -6 – 25 × 10 -6 ) = 794,3 kPa = 7,943 bar
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
