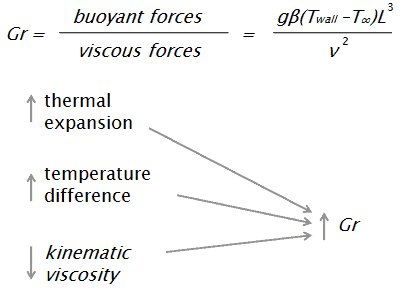
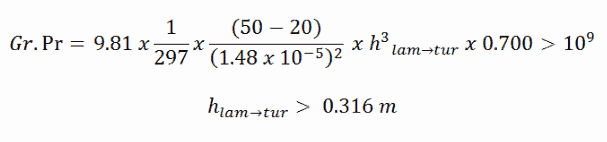¿Qué es el número de Grashof?
El número de Grashof es un número adimensional, llamado así por Franz Grashof. El número de Grashof se define como la relación entre la fuerza de flotación y la fuerza viscosa que actúa sobre un fluido en la capa límite de velocidad. Su papel en la convección natural es muy similar al del número de Reynolds en convección forzada.
La convección natural se usa si este movimiento y la mezcla son causados por variaciones de densidad resultantes de las diferencias de temperatura dentro del fluido. Por lo general, la densidad disminuye debido a un aumento de la temperatura y hace que el líquido suba. Este movimiento es causado por la fuerza de flotación. La fuerza principal que resiste el movimiento es la fuerza viscosa. El número de Grashof es una forma de cuantificar las fuerzas opuestas.
El número de Grashof se define como:
dónde:
g es la aceleración debido a la gravedad de la Tierra
β es el coeficiente de expansión térmica
T wall es la temperatura de la pared
T ∞ es la temperatura a granel
L es la longitud vertical
ν es la viscosidad cinemática.
Para gases β = 1 / T donde la temperatura está en K. Para líquidos se puede calcular β si se conoce la variación de densidad con temperatura a presión constante. Para una placa plana vertical, el flujo se vuelve turbulento para un valor de Gr.Pr> 10 9 . Al igual que en la convección forzada, la naturaleza microscópica del flujo y las correlaciones de convección son claramente diferentes en las regiones laminar y turbulenta.
El número de Grashof está estrechamente relacionado con el número de Rayleigh, que se define como el producto del número de Grashof, que describe la relación entre la flotabilidad y la viscosidad dentro de un fluido, y el número de Prandtl , que describe la relación entre la difusividad de momento y la difusividad térmica.
Ejemplo: número de Grashof
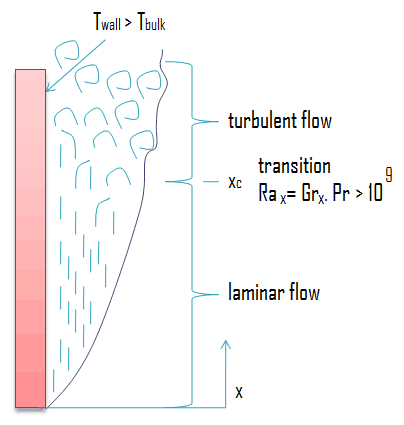 Una placa vertical se mantiene a 50 ° C en 20 ° C de aire. Determine la altura a la cual la capa límite se volverá turbulenta si la turbulencia se establece en Gr.Pr = 10 9 .
Una placa vertical se mantiene a 50 ° C en 20 ° C de aire. Determine la altura a la cual la capa límite se volverá turbulenta si la turbulencia se establece en Gr.Pr = 10 9 .
Solución:
Los valores de propiedad requeridos para este ejemplo son:
ν = 1,48 x 10-5 m 2 / s
ρ = 1,17 kg / m 3
Pr = 0.700
β = 1 / (273 + 20) = 1/293
Sabemos que la circulación natural se vuelve turbulenta en Gr.Pr> 10 9 , que se cumple a la siguiente altura:
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.