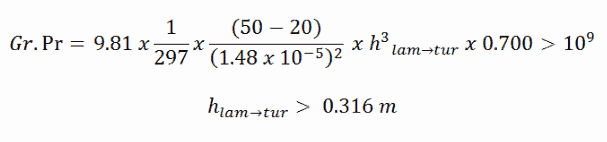O que é o número Grashof
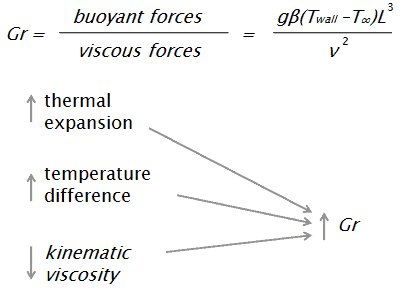
O número Grashof é um número sem dimensão, com o nome de Franz Grashof. O número de Grashof é definido como a razão entre a força flutuante e a viscosa que atua sobre um fluido na camada limite de velocidade. Seu papel na convecção natural é o mesmo que o número de Reynolds na convecção forçada.
Convecção natural é usada se esse movimento e mistura são causados por variações de densidade resultantes de diferenças de temperatura no fluido. Normalmente, a densidade diminui devido a um aumento de temperatura e faz com que o fluido suba. Este movimento é causado pela força flutuante. A força principal que resiste ao movimento é a força viscosa. O número de Grashof é uma maneira de quantificar as forças opostas.
O número de Grashof é definido como:
Onde:
g é aceleração devido à gravidade da Terra
β é o coeficiente de expansão térmica
Parede T é a temperatura da parede
T ∞ é a temperatura a granel
L é o comprimento vertical
ν é a viscosidade cinemática.
Para gases β = 1 / T onde a temperatura está em K. Para líquidos β pode ser calculado se for conhecida a variação da densidade com a temperatura a pressão constante. Para uma placa plana vertical, o fluxo fica turbulento pelo valor de Gr.Pr> 10 9 . Como na convecção forçada, a natureza microscópica das correlações de fluxo e convecção são distintamente diferentes nas regiões laminar e turbulenta.
O número de Grashof está intimamente relacionado ao número de Rayleigh, que é definido como o produto do número de Grashof, que descreve a relação entre flutuabilidade e viscosidade dentro de um fluido, e o número de Prandtl , que descreve a relação entre difusividade de momento e difusividade térmica.
Exemplo: Número Grashof
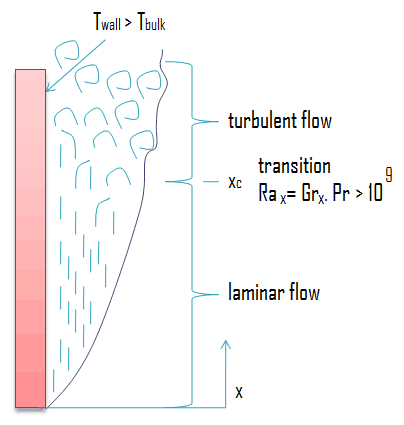 Uma placa vertical é mantida a 50 ° C em 20 ° C de ar. Determine a altura em que a camada limite ficará turbulenta se a turbulência se estabelecer em Gr.Pr = 10 9 .
Uma placa vertical é mantida a 50 ° C em 20 ° C de ar. Determine a altura em que a camada limite ficará turbulenta se a turbulência se estabelecer em Gr.Pr = 10 9 .
Solução:
Os valores da propriedade necessários para este exemplo são:
ν = 1,48 x 10-5 m 2 / s
ρ = 1,17 kg / m 3
Pr = 0,700
β = 1 / (273 + 20) = 1/293
Sabemos que a circulação natural se torna turbulenta em Gr.Pr> 10 9 , que é cumprida na seguinte altura:
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.