Eficiencia térmica para el ciclo de Atkinson
En general, la eficiencia térmica , η º , de cualquier motor de calor se define como la relación de la obra lo hace, W , para el calor de entrada a la alta temperatura, Q H .
La eficiencia térmica , η th , representa la fracción de calor , Q H , que se convierte en trabajo . Dado que la energía se conserva de acuerdo con la primera ley de la termodinámica y la energía no se puede convertir en trabajo por completo, la entrada de calor, Q H , debe ser igual al trabajo realizado, W, más el calor que se debe disipar como calor residual Q C en el ambiente. Por lo tanto, podemos reescribir la fórmula para la eficiencia térmica como:
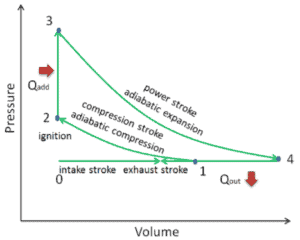
El calor absorbido ocurre durante la combustión de la mezcla de combustible y aire, cuando se produce la chispa, aproximadamente a un volumen constante. Dado que durante un proceso isocrórico no hay trabajo realizado por o sobre el sistema, la primera ley de la termodinámica dicta ∆U = ∆Q.
Por lo tanto, el calor agregado y rechazado están dados por:
Q add = mc v (T 3 – T 2 )
Q out = mc p (T 4 – T 1 )
Sustituyendo estas expresiones por el calor agregado y rechazado en la expresión por rendimientos de eficiencia térmica:
Además, se puede deducir que en términos de:
- la relación V 1 / V 2 , que se conoce como la relación de compresión – CR
- la relación V 4 / V 3 , que se conoce como la relación de expansión – ER.
- κ = c p / c v
La expresión para la eficiencia térmica usando estas características es:
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.