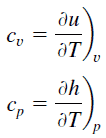¿Qué es la primera ley de la termodinámica? Definición

En palabras:

Forma de ecuación:

IntE _int = Q – W

donde E _int representa la energía interna del material, que depende solo del estado del material (temperatura, presión y volumen). Q es el calor neto agregado al sistema y W es el trabajo neto realizado por el sistema. Debemos ser cuidadosos y consistentes al seguir las convenciones de signos para Q y W. Como W en la ecuación es el trabajo realizado por el sistema, entonces si el trabajo se realiza en el sistema, W será negativo y E _int aumentará.

Del mismo modo, Q es positivo para el calor agregado al sistema, por lo que si el calor abandona el sistema, Q es negativo. Esto nos dice lo siguiente: la energía interna de un sistema tiende a aumentar si el sistema absorbe calor o si se realiza un trabajo positivo en el sistema. Por el contrario, la energía interna tiende a disminuir si el sistema pierde calor o si se realiza un trabajo negativo en el sistema. Debe agregarse que Q y W dependen de la ruta, mientras que E _int es independiente de la ruta.

Forma diferencial:

dE _int = dQ – dW

La energía interna E _int de un sistema tiende a aumentar si se agrega energía como calor Q y tiende a disminuir si se pierde energía como trabajo W realizado por el sistema.

Primera ley en términos de entalpía dH = dQ + Vdp

La entalpía se define para ser la suma de la energía interna E más el producto de la presión p y el volumen V . En muchos análisis termodinámicos aparece la suma de la energía interna U y el producto de la presión py el volumen V, por lo tanto, es conveniente dar a la combinación un nombre, entalpía y un símbolo distintivo, H.

H = U + pV

Ver también: entalpía

La primera ley de la termodinámica en términos de entalpía nos muestra por qué los ingenieros usan la entalpía en ciclos termodinámicos (por ejemplo, el ciclo de Brayton o el ciclo de Rankine ).

La forma clásica de la ley es la siguiente ecuación:

dU = dQ – dW

En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite .

Como H = U + pV , entonces dH = dU + pdV + Vdp y sustituimos dU = dH – pdV – Vdp en la forma clásica de la ley:dH – pdV – Vdp = dQ – pdV

Obtenemos la ley en términos de entalpía:

dH = dQ + Vdp

o

dH = TdS + Vdp

En esta ecuación, el término Vdp es un proceso de flujo de trabajo. Este trabajo,   Vdp , se utiliza para sistemas de flujo abierto como una turbina o una bomba en la que hay un “dp” , es decir, un cambio de presión. No hay cambios en el volumen de control . Como puede verse, esta forma de ley simplifica la descripción de la transferencia de energía . A presión constante , el cambio de entalpía es igual a la energía transferida del ambiente a través del calentamiento:

Proceso isobárico (Vdp = 0):

dH = dQ      →      Q = H ₂ – H ₁

En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema:

Proceso isentrópico (dQ = 0):

dH = Vdp      →      W = H ₂ – H ₁

Es obvio, será muy útil en el análisis de los dos ciclos termodinámicos utilizados en la ingeniería de energía, es decir, en el ciclo de Brayton y el ciclo de Rankine.

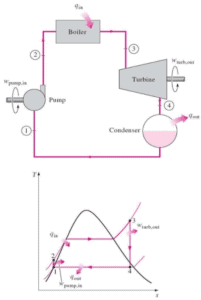
Ejemplo: primera ley de termodinámica y ciclo de Brayton

Supongamos el ciclo Brayton ideal que describe el funcionamiento de un motor de calor a presión constante . Los modernos motores de turbina de gas y los motores de inyección de aire también siguen el ciclo de Brayton. Este ciclo consta de cuatro procesos termodinámicos:

1. 

   Compresión isentrópica : el aire ambiente ingresa al compresor, donde se presuriza (1 → 2). El trabajo requerido para el compresor viene dado por W _C = H ₂ – H ₁ .

2. adición de calor isobárico : el aire comprimido pasa a través de una cámara de combustión, donde se quema el combustible y se calienta el aire u otro medio (2 → 3). Es un proceso de presión constante, ya que la cámara está abierta para fluir hacia adentro y hacia afuera. El calor neto agregado viene dado por Q _add = H ₃ – H ₂
3. Expansión isentrópica : el aire calentado y presurizado se expande en la turbina y entrega su energía. El trabajo realizado por la turbina viene dado por W _T = H ₄ – H ₃
4. rechazo de calor isobárico : el calor residual debe rechazarse para cerrar el ciclo. El calor neto rechazado viene dado por Q _re = H ₄ – H ₁

Como se puede ver, podemos describir y calcular (por ejemplo, eficiencia termodinámica) tales ciclos (de manera similar para el ciclo de Rankine ) usando entalpías .

Energía interna

En termodinámica, la energía interna (también llamada energía térmica ) se define como la energía asociada con formas microscópicas de energía . Es una cantidad extensa , depende del tamaño del sistema o de la cantidad de sustancia que contiene. La unidad SI de energía interna es el julio (J) . Es la energía contenida dentro del sistema, excluyendo la energía cinética de movimiento del sistema como un todo y la energía potencial del sistema. Las formas microscópicas de energía incluyen aquellas debidas a la rotación , vibración, traslación e interacciones.entre las moléculas de una sustancia. Ninguna de estas formas de energía se puede medir o evaluar directamente, pero se han desarrollado técnicas para evaluar el cambio en la suma total de todas estas formas microscópicas de energía.

Además, la energía se puede almacenar en los enlaces químicos entre los átomos que forman las moléculas. Este almacenamiento de energía a nivel atómico incluye energía asociada con estados orbitales de electrones, espín nuclear y fuerzas de unión en el núcleo.

Energía microscópica

La energía interna implica energía a escala microscópica . Se puede dividir en energía potencial microscópica, U _pot , y energía cinética microscópica, U _kin , componentes:

U = U _pot + U _kin

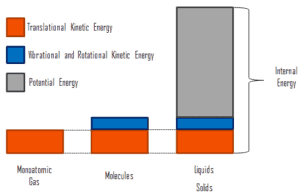donde la energía cinética microscópica, U _kin , involucra los movimientos de todas las partículas del sistema con respecto al marco del centro de masa. Para un gas monoatómico ideal , esto es solo la energía cinética traslacional del movimiento lineal de los átomos. Las partículas monoatómicas no giran ni vibran. El comportamiento del sistema está bien descrito por la teoría cinética de los gases. La teoría cinética se basa en el hecho de que durante una colisión elástica entre una molécula con alta energía cinética y otra con baja energía cinética, parte de la energía se transferirá a la molécula de menor energía cinética. Sin embargo, para los gases poliatómicos hay rotación yenergía cinética vibracional también.

La energía potencial microscópica, U _pot , involucra los enlaces químicos entre los átomos que forman las moléculas, las fuerzas de unión en el núcleo y también los campos de fuerza física dentro del sistema (por ejemplo, campos eléctricos o magnéticos).

En líquidos y sólidos hay un componente significativo de energía potencial asociado con las fuerzas de atracción intermoleculares .

Calor y trabajo

Hemos visto que la energía interna cambia con Q , que es el calor neto agregado al sistema y W , que es el trabajo neto realizado por el sistema. Ahora examinamos cómo el trabajo realizado y el calor agregado al sistema durante un proceso termodinámico dependen de los detalles de cómo se lleva a cabo el proceso.

Calor en termodinámica

Mientras que la energía interna se refiere a la energía total de todas las moléculas dentro del objeto, el calor es la cantidad de energía que fluye de un cuerpo a otro de forma espontánea debido a su diferencia de temperatura. El calor es una forma de energía, pero es energía en tránsito . El calor no es una propiedad de un sistema. Sin embargo, la transferencia de energía como calor ocurre a nivel molecular como resultado de una diferencia de temperatura .

Considere un bloque de metal a alta temperatura, que consiste en átomos que oscilan intensamente alrededor de sus posiciones promedio. A bajas temperaturas , los átomos continúan oscilando, pero con menos intensidad . Si un bloque de metal más caliente se pone en contacto con un bloque más frío, los átomos que oscilan intensamente en el borde del bloque más caliente emiten su energía cinética a los átomos menos oscilantes en el borde del bloque frío. En este caso, hay una transferencia de energía entre estos dos bloques y el calor fluye del bloque más caliente al más frío por estas vibraciones aleatorias.

En general, cuando dos objetos se ponen en contacto térmico , el calor fluirá entre ellos hasta que se equilibren entre sí. Cuando existe una diferencia de temperatura , el calor fluye espontáneamente del sistema más cálido al sistema más frío . La transferencia de calor ocurre por conducción o por radiación térmica . Cuando se detiene el flujo de calor , se dice que están a la misma temperatura . Luego se dice que están en equilibrio térmico .

Al igual que con el trabajo, la cantidad de calor transferido depende de la ruta y no simplemente de las condiciones iniciales y finales del sistema. En realidad, hay muchas maneras de llevar el gas del estado i al estado f.

Además, como con el trabajo, es importante distinguir entre el calor agregado a un sistema de su entorno y el calor eliminado de un sistema a su entorno. Q es positivo para el calor agregado al sistema, por lo que si el calor sale del sistema, Q es negativo. Debido a que W en la ecuación es el trabajo realizado por el sistema, entonces si el trabajo se realiza en el sistema, W será negativo y E _int aumentará.

El símbolo q a veces se usa para indicar el calor agregado o eliminado de un sistema por unidad de masa . Es igual al calor total (Q) agregado o eliminado dividido por la masa (m).

Capacidad calorífica

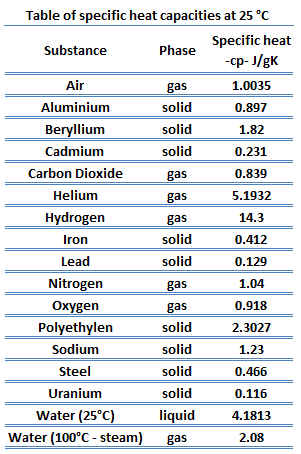Las diferentes sustancias se ven afectadas a diferentes magnitudes por la adición de calor . Cuando se agrega una cantidad determinada de calor a diferentes sustancias, sus temperaturas aumentan en diferentes cantidades. Esta constante de proporcionalidad entre el calor Q que el objeto absorbe o pierde y el cambio de temperatura resultante T del objeto se conoce como la capacidad calorífica C de un objeto.

C = Q / ΔT

La capacidad calorífica es una propiedad extensa de la materia, lo que significa que es proporcional al tamaño del sistema. La capacidad calorífica C tiene la unidad de energía por grado o energía por kelvin. Cuando se expresa el mismo fenómeno que una propiedad intensiva , la capacidad calorífica se divide por la cantidad de sustancia, masa o volumen, por lo que la cantidad es independiente del tamaño o extensión de la muestra.

Capacidad calorífica específica

La capacidad calorífica de una sustancia por unidad de masa se denomina capacidad calorífica específica (c _p ) de la sustancia. El subíndice p indica que la capacidad calorífica y la capacidad calorífica específica se aplican cuando el calor se agrega o elimina a presión constante .

c _p = Q / mΔT

Capacidad calorífica específica del gas ideal

En el modelo de gas ideal , las propiedades intensivas c _v y c _p se definen para sustancias compresibles puras y simples como derivadas parciales de la energía interna u (T, v) y entalpía h (T, p) , respectivamente:

donde los subíndices v y p denotan las variables mantenidas fijas durante la diferenciación. Las propiedades c _v y c _p se denominan calores específicos (o capacidades de calor ) porque, bajo ciertas condiciones especiales, relacionan el cambio de temperatura de un sistema con la cantidad de energía agregada por la transferencia de calor. Sus unidades SI son J / kg K o J / mol K . Se definen dos calores específicos para gases, uno para volumen constante (c _v ) y otro para presión constante (c _p ) .

Según la primera ley de la termodinámica , para un proceso de volumen constante con un gas ideal monoatómico, el calor específico molar será:

C _v = 3 / 2R = 12.5 J / mol K

porque

U = 3 / 2nRT

Se puede deducir que el calor específico molar a presión constante es:

C _p = C _v + R = 5 / 2R = 20.8 J / mol K

Este C _p es mayor que el calor específico molar a volumen constante C _v , porque ahora se debe suministrar energía no solo para elevar la temperatura del gas sino también para que el gas funcione porque en este caso el volumen cambia.

Calor latente de vaporización

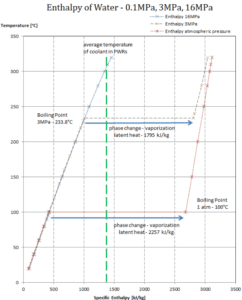
En general, cuando un material cambia de fase de sólido a líquido, o de líquido a gas, una cierta cantidad de energía está involucrada en este cambio de fase. En caso de cambio de fase de líquido a gas, esta cantidad de energía se conoce como entalpía de vaporización , (símbolo ∆H _vap ; unidad: J) también conocido como calor (latente) de vaporización o calor de evaporación. El calor latente es la cantidad de calor agregado o eliminado de una sustancia para producir un cambio de fase. Esta energía descompone las fuerzas de atracción intermoleculares, y también debe proporcionar la energía necesaria para expandir el gas (el trabajo pΔV) Cuando se agrega calor latente, no ocurre cambio de temperatura. La entalpía de la vaporización es una función de la presión a la que tiene lugar esa transformación.

Calor latente de vaporización – agua a 0.1 MPa (presión atmosférica)

h _lg = 2257 kJ / kg

Calor latente de vaporización: agua a 3 MPa (presión dentro de un generador de vapor)

h _lg = 1795 kJ / kg

Calor latente de vaporización: agua a 16 MPa (presión dentro de un presurizador )

h _lg = 931 kJ / kg

El calor de vaporización disminuye al aumentar la presión, mientras que aumenta el punto de ebullición . Se desvanece por completo en un cierto punto llamado punto crítico . Por encima del punto crítico, las fases líquida y de vapor son indistinguibles, y la sustancia se llama fluido supercrítico .

El calor de vaporización es el calor requerido para vaporizar completamente una unidad de líquido saturado (o condensar una unidad de masa de vapor saturado) y es igual a h _lg = h _g – h _l .

El calor necesario para derretir (o congelar) una unidad de masa en la sustancia a presión constante es el calor de fusión y es igual a h _sl = h _l – h _s , donde h _s es la entalpía del sólido saturado y h _l Es la entalpía del líquido saturado.

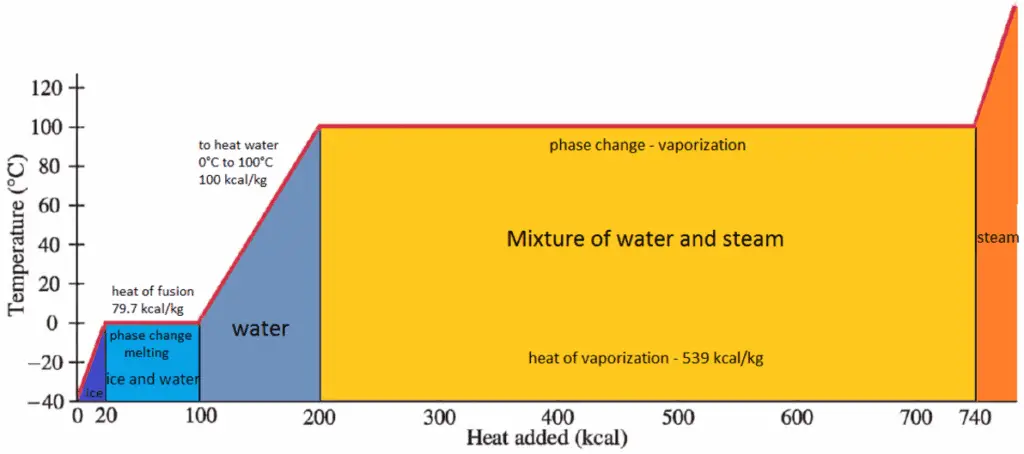
Trabajar en termodinámica

En termodinámica, el trabajo realizado por un sistema es la energía transferida por el sistema a su entorno. La energía cinética, la energía potencial y la energía interna son formas de energía que son propiedades de un sistema. El trabajo es una forma de energía , pero es energía en tránsito . Un sistema no contiene trabajo, el trabajo es un proceso realizado por o en un sistema. En general, el trabajo se define para sistemas mecánicos como la acción de una fuerza sobre un objeto a través de una distancia.

W = F. re

dónde:

W = trabajo (J)

F = fuerza (N)

d = desplazamiento (m)

pΔV trabajo

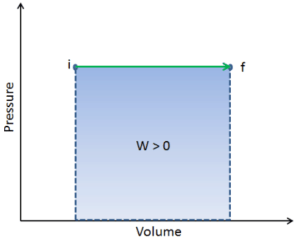
El trabajo de presión-volumen (o trabajo pΔV ) ocurre cuando cambia el volumen V de un sistema. El trabajo pΔV es igual al área bajo la curva de proceso trazada en el diagrama de presión-volumen. También se conoce como el trabajo de límites . El trabajo de límite  ocurre porque la masa de la sustancia contenida dentro del límite del sistema provoca una fuerza, la presión multiplicada por el área de la superficie, para actuar sobre la superficie del límite y hacer que se mueva. El trabajo de límite  (o  pΔV Work ) ocurre cuando el  volumen V de un sistema cambia . Se utiliza para calcular el trabajo de desplazamiento del pistón en un  sistema cerrado.    . Esto es lo que sucede cuando el  vapor o el gas contenido en un dispositivo de pistón-cilindro se expande contra el pistón y lo obliga a moverse.

Ejemplo:

Considere un pistón sin fricción que se utiliza para proporcionar una presión constante de 500 kPa en un cilindro que contiene vapor de agua ( vapor sobrecalentado ) de un volumen de 2 m ³  a 500 K .

Calcule la temperatura final, si se agregan 3000 kJ de calor .

Solución:

Usando tablas de vapor , sabemos que la entalpía específica de dicho vapor (500 kPa; 500 K) es de aproximadamente 2912 kJ / kg . Como en esta condición el vapor tiene una densidad de 2.2 kg / m ³ , entonces sabemos que hay alrededor de 4.4 kg de vapor en el pistón a una entalpía de 2912 kJ / kg x 4.4 kg = 12812 kJ .

Cuando usamos simplemente Q = H ₂ – H ₁ , la entalpía de vapor resultante será:

H ₂ = H ₁ + Q = 15812 kJ

De las mesas de vapor , dicho vapor sobrecalentado (15812 / 4.4 = 3593 kJ / kg) tendrá una temperatura de 828 K (555 ° C) . Dado que en esta entalpía el vapor tiene una densidad de 1.31 kg / m ³ , es obvio que se ha expandido aproximadamente 2.2 / 1.31 = 1.67 (+ 67%). Por lo tanto, el volumen resultante es 2 m ³ x 1.67 = 3.34 m ³ y ∆V = 3.34 m ³ – 2 m ³ = 1.34 m ³ .

La parte p∆V de la entalpía, es decir, el trabajo realizado es:

W = p∆V = 500 000 Pa x 1.34 m ³ = 670 kJ

———–

Durante el cambio de volumen , la presión y la temperatura también pueden cambiar. Para calcular tales procesos, necesitaríamos saber cómo la presión varía con el volumen para el proceso real por el cual el sistema cambia del estado i al estado f . La primera ley de la termodinámica y el trabajo se pueden expresar como:

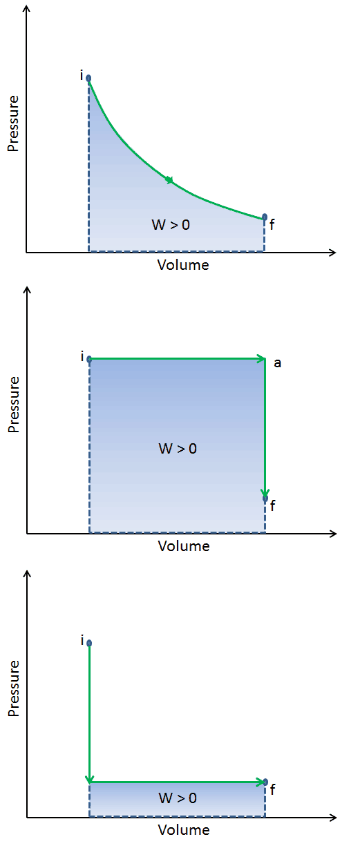
Cuando un sistema termodinámico cambia de un estado inicial a un estado final , pasa a través de una serie de estados intermedios . Llamamos a esta serie de estados un camino . Siempre hay infinitas posibilidades diferentes para estos estados intermedios. Cuando todos son estados de equilibrio, la ruta se puede trazar en un diagrama pV . Una de las conclusiones más importantes es que:

El trabajo realizado por el sistema depende no solo de los estados inicial y final, sino también de los estados intermedios, es decir, de la ruta.

Q y W dependen de la ruta, mientras que ΔE _int es independiente de la ruta. Como se puede ver en la imagen (diagrama pV), el trabajo es una variable dependiente de la ruta. El área azul representa el trabajo pΔV realizado por un sistema a medida que pasa de un estado inicial i a un estado final f. El trabajo W es positivo porque aumenta el volumen del sistema. El segundo proceso muestra que el trabajo es mayor y que depende de la ruta del proceso.

Además, podemos llevar el sistema a través de una serie de estados que forman un circuito cerrado , como i ⇒ f ⇒ i . En este caso, el estado final es el mismo que el estado inicial , pero el trabajo total realizado por el sistema no es cero . Un valor positivo para el trabajo indica que el trabajo lo realiza el sistema en su entorno. Un valor negativo indica que el trabajo se realiza en el sistema por su entorno.

Ejemplo: trabajo específico de turbina

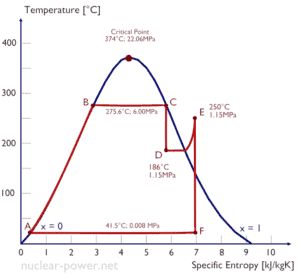
Una etapa de alta presión de la turbina de vapor funciona en estado estable con condiciones de entrada de   6 MPa , t = 275.6 ° C , x = 1 (punto C). Vapor hojas esta etapa de la turbina a una presión de 1,15 MPa , 186 ° C y x = 0,87 (punto D). Calcule la diferencia de entalpía entre estos dos estados. Determinar la transferencia de trabajo específica.

La entalpía para el estado C puede seleccionarse directamente de las tablas de vapor , mientras que la entalpía para el estado D debe calcularse utilizando la calidad del vapor :

h _{1, húmedo} = 2785 kJ / kg

h _{2, húmedo} = h _{2, s} x + (1 – x) h _{2, l}  = 2782. 0.87 + (1 – 0.87). 790 = 2420 + 103 = 2523 kJ / kg

Δh = 262 kJ / kg

Dado que en el proceso adiabático dh = dw , Δh = 262 kJ / kg es el trabajo específico de la turbina .

Cuatro casos especiales de la primera ley de la termodinámica

La primera ley de la termodinámica encuentra aplicación en varios casos especiales:

Proceso adiabático:

Un proceso adiabático es aquel en el que no hay transferencia de calor dentro o fuera del sistema. Se produce muy rápidamente o un sistema está bien aislado de que no se transfiere energía a medida que se produce calor entre el sistema y su entorno. Por lo tanto, dQ = 0 en la primera ley de la termodinámica, que es entonces:

dQ = 0, dE _int = – dW

Proceso isocorico:

Un proceso isocrórico es aquel en el que no hay cambio en el volumen . Un proceso isocrórico es un proceso de volumen constante. Cuando el volumen de un sistema termodinámico es constante, no funciona en su entorno. Por lo tanto, dW = 0 en la primera ley de la termodinámica, que es entonces:

dW = 0, dE _int = dQ

En un proceso isocrórico , toda la energía agregada como calor (es decir, Q es positiva) permanece en el sistema como un aumento de la energía interna ( aumento de la temperatura ).

Proceso Cíclico:

Un proceso que finalmente devuelve un sistema a su estado inicial se denomina proceso cíclico . Al final de un ciclo, todas las propiedades tienen el mismo valor que tenían al principio.

Para tal proceso, el estado final es el mismo que el estado inicial, por lo que el cambio total de energía interna debe ser cero . El vapor (agua) que circula a través de un circuito cerrado de enfriamiento experimenta un ciclo. La primera ley de la termodinámica es entonces:

dE _int = 0, dQ = dW

Por lo tanto, el trabajo neto realizado durante el proceso debe ser exactamente igual a la cantidad neta de energía transferida como calor.

Expansión gratis:

Este es un  proceso adiabático en el que no se produce transferencia de calor entre el sistema y su entorno y no se realiza ningún trabajo en el sistema. Estos tipos de procesos adiabáticos se denominan expansión libre . Es un proceso irreversible en el que un gas se expande en una cámara de evacuación aislada. También se llama expansión Joule . Para un gas ideal, la temperatura no cambia (ver: Segunda Ley de Joule ), sin embargo, los gases reales experimentan un cambio de temperatura durante la expansión libre. En expansión libre, Q = W = 0, y la primera ley requiere que:

dE _int = 0

No se puede trazar una expansión libre en un diagrama PV, porque el proceso es rápido, no cuasiestático. Los estados intermedios no son estados de equilibrio y, por lo tanto, la presión no está claramente definida.