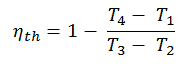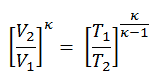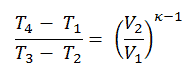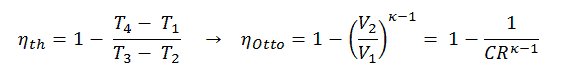Eficiencia térmica para el ciclo Otto
En general, la eficiencia térmica , η º , de cualquier motor de calor se define como la relación de la obra lo hace, W , para el calor de entrada a la alta temperatura, Q H .
La eficiencia térmica , η th , representa la fracción de calor , Q H , que se convierte en trabajo . Dado que la energía se conserva de acuerdo con la primera ley de la termodinámica y la energía no se puede convertir en trabajo por completo, la entrada de calor, Q H , debe ser igual al trabajo realizado, W, más el calor que se debe disipar como calor residual Q C en el ambiente. Por lo tanto, podemos reescribir la fórmula para la eficiencia térmica como:
El calor absorbido ocurre durante la combustión de la mezcla de combustible y aire, cuando se produce la chispa, aproximadamente a un volumen constante. Dado que durante un proceso isocrórico no hay trabajo realizado por o sobre el sistema, la primera ley de la termodinámica dicta ∆U = ∆Q. Por lo tanto, el calor agregado y rechazado están dados por:
Q add = mc v (T 3 – T 2 )
Q out = mc v (T 4 – T 1 )
Sustituyendo estas expresiones por el calor agregado y rechazado en la expresión por rendimientos de eficiencia térmica:
Podemos simplificar la expresión anterior usando el hecho de que los procesos 1 → 2 y de 3 → 4 son adiabáticos y para un proceso adiabático la siguiente fórmula p, V, T es válida:
Se puede derivar que:
En esta ecuación, la relación V 1 / V 2 se conoce como la relación de compresión, CR . Cuando reescribimos la expresión de eficiencia térmica usando la relación de compresión, concluimos que la eficiencia térmica del ciclo Otto estándar de aire es una función de la relación de compresión y κ = c p / c v .
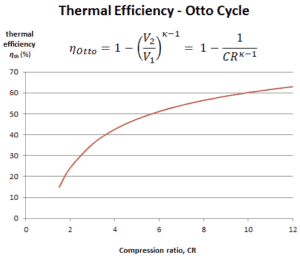
Es una conclusión muy útil, porque es deseable lograr una alta relación de compresión para extraer más energía mecánica de una masa dada de mezcla aire-combustible. Una relación de compresión más alta permite alcanzar la misma temperatura de combustión con menos combustible, al tiempo que proporciona un ciclo de expansión más largo. Esto crea más potencia mecánica y reduce la temperatura de escape . Disminuir la temperatura de escape provoca la disminución de la energía rechazada a la atmósfera. Esta relación se muestra en la figura para κ = 1.4, que representa el aire ambiente.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.