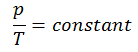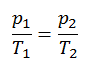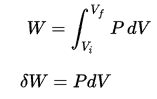Proceso isocórico – Proceso isométrico
Un proceso isocórico es un proceso termodinámico, en el que el volumen del sistema cerrado permanece constante (V = constante). Describe el comportamiento del gas dentro del contenedor, que no se puede deformar. Dado que el volumen permanece constante, la transferencia de calor dentro o fuera del sistema no hace funcionar el p∆V , sino que solo cambia la energía interna (la temperatura) del sistema.
Para un gas ideal y un proceso politrópico , el caso n ➝ ∞ corresponde a un proceso isocórico (volumen constante) . A diferencia del proceso adiabático , en el que n = y un sistema no intercambia calor con su entorno (Q = 0; W ≠ 0 ) , en un proceso isocórico hay un cambio en la energía interna (debido a ∆T ≠ 0) y por lo tanto, ΔU ≠ 0 (para gases ideales) y (Q ≠ 0; W = 0 ).
En la ingeniería de motores de combustión interna , los procesos isocóricos son muy importantes por sus ciclos termodinámicos (ciclo Otto y Diesel), por lo que el estudio de este proceso es crucial para la ingeniería automotriz.
Proceso isocórico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como trabajo de contorno . Luego:
dU = dQ – pdV
En el proceso isocórico y el gas ideal, todo el calor agregado al sistema se utilizará para aumentar la energía interna.
Proceso isocórico (pdV = 0):
dU = dQ (para gas ideal)
Proceso isocórico: ecuación de gas ideal
Ver también: ¿Qué es un gas ideal?
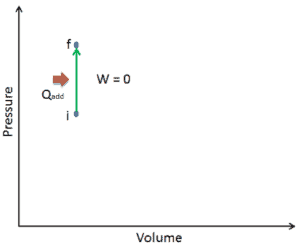 Supongamos una adición de calor isocrórica en un gas ideal. En un gas ideal , las moléculas no tienen volumen y no interactúan. Según la ley de los gases ideales , la presión varía linealmente con la temperatura y la cantidad, e inversamente con el volumen .
Supongamos una adición de calor isocrórica en un gas ideal. En un gas ideal , las moléculas no tienen volumen y no interactúan. Según la ley de los gases ideales , la presión varía linealmente con la temperatura y la cantidad, e inversamente con el volumen .
pV = nRT
dónde:
- p es la presión absoluta del gas
- n es la cantidad de sustancia
- T es la temperatura absoluta
- V es el volumen
- R es la constante de gas ideal, o universal, igual al producto de la constante de Boltzmann y la constante de Avogadro,
En esta ecuación, el símbolo R es una constante llamada constante de gas universal que tiene el mismo valor para todos los gases, es decir, R = 8.31 J / mol K.
El proceso isocrórico se puede expresar con la ley de los gases ideales como:
o
En un diagrama pV , el proceso ocurre a lo largo de una línea horizontal que tiene la ecuación V = constante.
El trabajo de presión-volumen del sistema cerrado se define como:
Como el proceso es isocrórico , dV = 0 , el trabajo de presión-volumen es igual a cero . Según el modelo de gas ideal, la energía interna se puede calcular mediante:
∆U = mc v ∆T
donde la propiedad c v (J / mol K) se denomina calor específico (o capacidad calorífica ) a un volumen constante porque, bajo ciertas condiciones especiales (volumen constante), relaciona el cambio de temperatura de un sistema con la cantidad de energía agregada por transferencia de calor.
Como no hay trabajo realizado por o sobre el sistema, la primera ley de la termodinámica dicta ∆U = ∆Q. Por lo tanto:
Q = mc v ∆T
Ver también: Calor específico a volumen constante y presión constante
Ver también: fórmula de Mayer
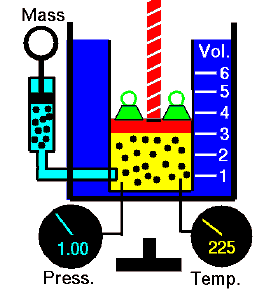
Ley de Guy-Lussac
La Ley de Guy-Lussac o la Ley de Presión, una de las leyes del gas, establece que:
Para una masa fija de gas a volumen constante, la presión es directamente proporcional a la temperatura Kelvin.
Eso significa que, por ejemplo, si duplica la temperatura, duplicará la presión. Si reduce a la mitad la temperatura, reducirá a la mitad la presión.
Puede expresar esto matemáticamente como:
p = constante. T
Sí, parece ser idéntico al proceso isocrórico del gas ideal. Estos resultados son totalmente consistentes con la ley de los gases ideales, que determina que la constante es igual a nR / V. Si reorganiza la ecuación pV = nRT dividiendo ambos lados por V, obtendrá:
p = nR / V. T
donde nR / V es constante y:
- p es la presión absoluta del gas
- n es la cantidad de sustancia
- T es la temperatura absoluta
- V es el volumen
- R es la constante de gas ideal o universal, igual al producto de la constante de Boltzmann y la constante de Avogadro
Ejemplo de proceso isocrórico: adición de calor isocrórico
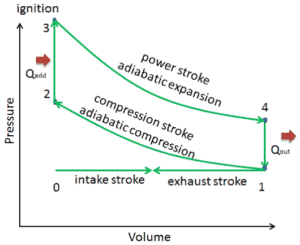 Supongamos el ciclo Otto , que es uno de los ciclos termodinámicos más comunes que se pueden encontrar en los motores de automóviles . Este ciclo supone que la adición de calor ocurre instantáneamente ( entre 2 → 3 ) mientras el pistón está en el punto muerto superior. Este proceso se considera isocrórico.
Supongamos el ciclo Otto , que es uno de los ciclos termodinámicos más comunes que se pueden encontrar en los motores de automóviles . Este ciclo supone que la adición de calor ocurre instantáneamente ( entre 2 → 3 ) mientras el pistón está en el punto muerto superior. Este proceso se considera isocrórico.
Los procesos 2 → 3 y 4 → 1 son procesos isocróricos , en los que el calor se transfiere al sistema entre 2 → 3 y fuera del sistema entre 4 → 1. Durante estos procesos no se realiza ningún trabajo en el sistema ni se extrae del sistema. . El proceso isocrórico 2 → 3 está destinado a representar la ignición de la mezcla de combustible y aire y la posterior combustión rápida.